题目内容
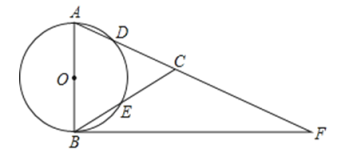
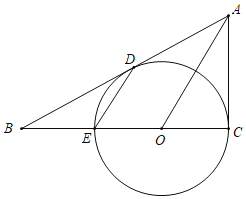
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 、
、![]() 是
是![]() 上的两点,
上的两点,![]() ,
,![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]()

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]()
(3)若![]() ,
,![]() ,求弦
,求弦![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)连接OC,可证得∠CAD=∠BCD,由∠CAD+∠ABC=90°,可得出∠OCD=90°,即结论得证;
(2)证明△ABC≌△AFC可得CB=CF,又CB=CE,则CE=CF;
(3)证明△CBD∽△DCA,可求出DA的长,求出AB长,设BC=a,AC=![]() a,则由勾股定理可得AC的长.
a,则由勾股定理可得AC的长.
(1)连![]() ,
,

∵![]() ,
,
∴![]() ,
,
又![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,且
,且![]() 过半径
过半径![]() 的外端点,
的外端点,
∴![]() 是
是![]() 的切线;
的切线;
(2)在![]() 和
和![]() 中,
中,![]() ,
,
![]() ,
,![]() 为公共边,
为公共边,
∴![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ;
;
(3)∵∠BCD=∠CAD,∠ADC=∠CDB,
∴△CBD∽△DCA,
∴![]() ,
,
∴![]() ,
,
∴DA=2,
∴AB=AD-BD=2-1=1,
设BC=a,AC=![]() a,由勾股定理可得:a2+(
a,由勾股定理可得:a2+(![]() a)2=12,
a)2=12,
解得:a=![]() ,
,
∴AC=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目