Question

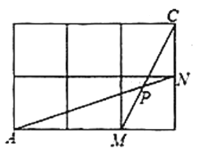
【题目】如图，是大小相等的边长为1的正方形构成的网格，，，，均为格点.与交于点.

[1].的值为_________.

[2].现只有无刻度的直尺，请在给定的网格中作出一个格点三角形.要求：①三角形中含有与大小相等的角；②可借助该三角形求得的三角函数值.请并在横线上简单说明你的作图方法.____________．

Answer 1

【答案】 取格点，连结，，则即为所求.（或者取格点，连结，，则即为所求.）

【解析】

[1].设AN与网格的交点为D，根据DM//BC证出和,得出比例式，再根据CN=BN即可得出的值

[2]. .过点N作NG, 过点P作,垂足分别为G、H，根据求出CP的长，再根据求出PH的长，根据等积法求出NG,再用勾股定理得出GC的长，从而求出PG=GN,得出，所以在网格中找出等腰直角三角形就符合题意．

[1].设AN与网格的交点为D，

∵DM//BC，

∴，,

∴,

∵CN=BN,

∴,

故答案为：

[2] 过点N作NG, 过点P作,垂足分别为G、H,

根据勾股定理得：CM=,

∵

∴

∵, ∴

∴

∴，∴,

∵

∴,根据勾股定理得：,

∴PG=PC-GC==,

∴是等腰直角三角形，

∴

法一：取格点，连结，，可得是等腰直角三角形，则即为所求.

法二：取格点，连结，，可得是等腰直角三角形，则即为所求.