��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������![]() ��
��![]() �ύ��
�ύ��![]() ����
����![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ������
������![]() ��
��
��1����������ߵĽ���ʽ����д�����ĶԳ��
��2����![]() Ϊ�����߶Գ�����һ�㣬����
Ϊ�����߶Գ�����һ�㣬����![]() ����
����![]() �����
�����![]() �����ꣻ
�����ꣻ
��3����֪![]() ����
����![]() ����������һ�����㣨����
����������һ�����㣨����![]() ��������
��������![]() ����
����![]() ��������ֵ����ʱ��
��������ֵ����ʱ��![]() �����꣮
�����꣮
��4������![]() Ϊ�����߶Գ�����һ�㣬���������Ƿ���ڵ�
Ϊ�����߶Գ�����һ�㣬���������Ƿ���ڵ�![]() ��ʹ����
��ʹ����![]() Ϊ������ı�����ƽ���ı��Σ������ڣ���ֱ��д���������������ĵ�
Ϊ������ı�����ƽ���ı��Σ������ڣ���ֱ��д���������������ĵ�![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��![]() ���Գ���
���Գ���![]() ����2��
����2��![]() ����3����������ֵ��
����3����������ֵ��![]() ��
��![]() ����4�����ڵ�
����4�����ڵ�![]() ʹ����
ʹ����![]() Ϊ������ı�����ƽ���ı��Σ�
Ϊ������ı�����ƽ���ı��Σ�![]() ��
��![]() ��
��![]() .
.
��������
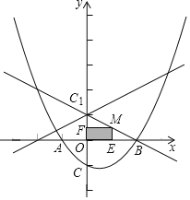
��1������A��-1��0����B��3��0������y=ax2+bx+2���ɣ�
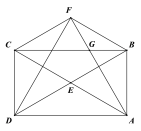
��2������D��DG��y����G����DH��x����H�����D��1��y������Rt��CGD�У�CD2=CG2+GD2=��2-y��2+1����Rt��BHD�У�BD2=BH2+HD2=4+y2������֤��CD=BD��������y��ֵ��
��3������E��EQ��y���ڵ�Q������F��ֱ��FR��y����R������E��FP��FR��P��֤���ı���QRPE�Ǿ��Σ�����S��CEF=S����QRPE-S��CRF-S��EFP��������ɣ�
��4������ƽ���ı��ζԱ�ƽ������ȵ����ʿ��Եõ����ڵ�Mʹ����B��C��M��NΪ������ı�����ƽ���ı��Σ���M��2��2����M��4��- ![]() ����M��-2��-
����M��-2��-![]() ����
����
�⣺��1������![]() ����
����![]() ��
��
�ɵ�![]() ��
��
![]() ��
��
![]() �Գ���
�Գ���![]() ��
��
��2����ͼ1������![]() ��
��![]() ����
����![]() ����
����![]() ����
����![]() ��
��

���![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
��![]() ��
�У�![]()
![]() ��
��
![]()
![]()
![]() ��
��
![]() ��
��
��3����ͼ2������![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��ֱ��
��ֱ��![]() ����
����![]() ������
������![]() ��
��![]() ��
��![]() ��
��

![]() ��
��
![]() �ı���
�ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
![]() ��
��
![]() ��
��
![]()
![]()
![]() ��
��
![]()
![]() ��
��![]() ʱ����������ֵ��
ʱ����������ֵ��![]() ��
��
��ʱ![]() ��
��
��4�����ڵ�![]() ʹ����
ʹ����![]() Ϊ������ı�����ƽ���ı��Σ�
Ϊ������ı�����ƽ���ı��Σ�
��![]() ��
��
���ı���![]() ��ƽ���ı���ʱ��
��ƽ���ı���ʱ��
![]()
![]()
![]()
���ı���![]() ʱƽ���ı���ʱ��
ʱƽ���ı���ʱ��
![]()
![]() ��
��
![]() ��
��
���ı���![]() ʱƽ���ı���ʱ��
ʱƽ���ı���ʱ��
![]() ��
��
![]() ��
��
![]() ��
��
����������![]() ��
��![]() ��
��![]() ��
��

 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�