ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌвбжЊЪ§жсЩЯЕу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ,Еу
,Еу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ,вд
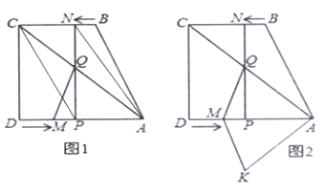
,вд![]() ЮЊБпдкЪ§жсЕФЩЯЗНзїе§ЗНаЮABCD.ЖЏЕу
ЮЊБпдкЪ§жсЕФЩЯЗНзїе§ЗНаЮABCD.ЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂ,вдУПУы
ГіЗЂ,вдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсе§ЗНЯђдШЫйдЫЖЏЃЌЭЌЪБЖЏЕу
ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсе§ЗНЯђдШЫйдЫЖЏЃЌЭЌЪБЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂ,вдУПУы
ГіЗЂ,вдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕу
ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕу![]() дШЫйдЫЖЏЃЌЕНДя
дШЫйдЫЖЏЃЌЕНДя![]() ЕуКѓдйвдЭЌбљЕФЫйЖШбиЪ§жсе§ЗНЯђдШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ
ЕуКѓдйвдЭЌбљЕФЫйЖШбиЪ§жсе§ЗНЯђдШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ![]() Уы
Уы![]() .
.
(1)ШєЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() .ЩЯдЫЖЏЃЌЕБtЮЊКЮжЕЪБ,
.ЩЯдЫЖЏЃЌЕБtЮЊКЮжЕЪБ,![]() ?
?
(2)ШєЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯдЫЖЏЃЌСЌНг
ЩЯдЫЖЏЃЌСЌНг![]() ,ЕБtЮЊКЮжЕЪБ,Ш§НЧаЮ
,ЕБtЮЊКЮжЕЪБ,Ш§НЧаЮ![]() ЕФУцЛ§ЕШгке§ЗНаЮ
ЕФУцЛ§ЕШгке§ЗНаЮ![]() УцЛ§ЕФ
УцЛ§ЕФ![]() ?
?
(3)дкЕу![]() КЭЕу
КЭЕу![]() дЫЖЏЕФЙ§ГЬжаЃЌЕБ
дЫЖЏЕФЙ§ГЬжаЃЌЕБ![]() ЮЊКЮжЕЪБЃЌЕу
ЮЊКЮжЕЪБЃЌЕу![]() гыЕу
гыЕу![]() ЧЁКУжиКЯ?
ЧЁКУжиКЯ?
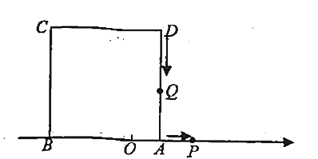
(4)ЕБЕу![]() дкЪ§жсЩЯдЫЖЏЪБЃЌЪЧЗёДцдкФГ-ЪБПЬt,ЪЙЕУЯпЖЮ
дкЪ§жсЩЯдЫЖЏЪБЃЌЪЧЗёДцдкФГ-ЪБПЬt,ЪЙЕУЯпЖЮ![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ,ШєДцдкЃЌЧѓГі
,ШєДцдкЃЌЧѓГі![]() ЕФжЕ;ШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФжЕ;ШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
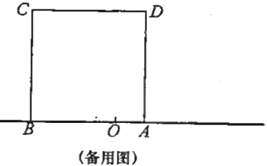
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ4ЃЛЃЈ4ЃЉДцдкЃЌt=3Лђ5ЃЌРэгЩМћЯъНт.
ЃЛЃЈ3ЃЉ4ЃЛЃЈ4ЃЉДцдкЃЌt=3Лђ5ЃЌРэгЩМћЯъНт.
ЁОНтЮіЁП
(1)гЩЪ§жсЩЯЕу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ,Еу
,Еу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ,вд
,вд![]() ЮЊБпдкЪ§жсЕФЩЯЗНзїе§ЗНаЮABCDЃЌ
ЮЊБпдкЪ§жсЕФЩЯЗНзїе§ЗНаЮABCDЃЌ![]() ЃЌСаГіЗНГЬЃЌМДПЩЧѓНтЃЛ
ЃЌСаГіЗНГЬЃЌМДПЩЧѓНтЃЛ
(2)ИљОнШ§НЧаЮ![]() ЕФУцЛ§ЕШгке§ЗНаЮ
ЕФУцЛ§ЕШгке§ЗНаЮ![]() УцЛ§ЕФ
УцЛ§ЕФ![]() ЃЌСаГіЗНГЬЃЌМДПЩЃЛ
ЃЌСаГіЗНГЬЃЌМДПЩЃЛ
(3)ИљОнЕШСПЙиЯЕЃЌСаГіЗНГЬМДПЩЧѓНтЃЛ
(4)ЗжСНжжЧщПіЃКЂйЕБЕуQдкЕуPЕФзѓВрЪБЃЌ ЂкЕБЕуQдкЕуPЕФгвВрЪБЃЌЗжБ№СаГіЗНГЬЃЌМДПЩЧѓНт.
ЃЈ1ЃЉЁпЪ§жсЩЯЕу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ,Еу
,Еу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ,вд
,вд![]() ЮЊБпдкЪ§жсЕФЩЯЗНзїе§ЗНаЮABCDЃЌ
ЮЊБпдкЪ§жсЕФЩЯЗНзїе§ЗНаЮABCDЃЌ
ЁрAD=AB=4ЃЌ
ЁрAQ=4-2tЃЌAP=tЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр4-2t =tЃЌНтЕУЃКt=![]() ЃЌ
ЃЌ
ЁрЕБt=![]() УыЪБЃЌ
УыЪБЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпAQ=4-2tЃЌAB=4ЃЌ
Ёр![]() ЃЌе§ЗНаЮ
ЃЌе§ЗНаЮ![]() УцЛ§=4ЁС4=16ЃЌ
УцЛ§=4ЁС4=16ЃЌ
Ёр8-4t=![]() ЃЌНтЕУЃКt=
ЃЌНтЕУЃКt=![]() ЃЌ
ЃЌ
ЁрЕБt=![]() УыЪБЃЌШ§НЧаЮ
УыЪБЃЌШ§НЧаЮ![]() ЕФУцЛ§ЕШгке§ЗНаЮ
ЕФУцЛ§ЕШгке§ЗНаЮ![]() УцЛ§ЕФ
УцЛ§ЕФ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉИљОнЬтвтЕУЃК2t-4=tЃЌНтЕУЃКt=4ЃЌ
ЁрЕБt=4УыЪБЃЌЕу![]() гыЕу
гыЕу![]() ЧЁКУжиКЯЃЛ
ЧЁКУжиКЯЃЛ
ЃЈ4ЃЉЂйЕБЕуQдкЕуPЕФзѓВрЪБЃЌt-ЃЈ2t-4ЃЉ=1ЃЌНтЕУЃКt=3ЃЌ
ЂкЕБЕуQдкЕуPЕФгвВрЪБЃЌЃЈ2t-4ЃЉ-t=1ЃЌНтЕУЃКt=5ЃЌ
ЁрЕБt=3УыЛђ5УыЪБЃЌЯпЖЮ![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() .
.

ЁОЬтФПЁПФГФІЭаГЕГЇБОжмМЦЛЎУПШеЩњВњ450СОФІЭаГЕЃЌгЩгкЙЄШЫЪЕааТжанЃЌ УПШеЩЯАрШЫЪ§ВЛвЛЖЈЯрЕШЃЌЪЕМЪУПШеЩњВњСПгыМЦЛЎСПЯрБШЧщПіШчЯТБэЃК [діМгЕФСОЪ§ЮЊе§Ъ§ЃЌМѕЩйЕФСОЪ§ЮЊИКЪ§]
аЧЦк | вЛ | Жў | Ш§ | ЫФ | Юх | Сљ | Ше |
діМѕ | Ѓ5 | +7 | Ѓ3 | +4 | +10 | Ѓ9 | Ѓ25 |
ЃЈ1ЃЉБОжмаЧЦкСљЩњВњЖрЩйСОФІЭаГЕЃП
ЃЈ2ЃЉБОжмзмВњСПгыМЦЛЎВњСПЯрБШЃЌЪЧдіМгСЫЛЙЪЧМѕЩйСЫЃПЮЊЪВУД?
ЃЈ3ЃЉВњСПзюЖрЕФФЧЬьБШВњСПзюЩйЕФФЧЬьЖрЩњВњЖрЩйСОЃП