Question

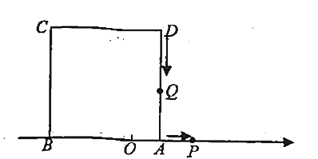
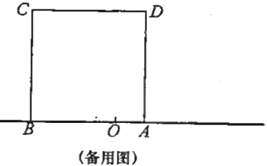
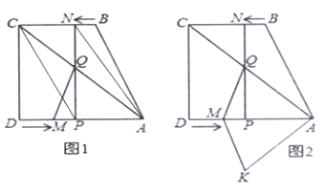
【题目】如图1，四边形中，，，，，点从点出发，以每秒2个单位长度的速度向点运动，同时，点从点出发，以每秒1个单位长度的速度向点运动.其中一个动点到达终点时，另一个动点也随之停止运动.过点作于点，连接交于点，连接，设运动时间为秒.

(1)连接、，当为何值时，四边形为平行四边形；

(2)求出点到的距离；

(3)如图2，将沿翻折，得，是否存在某时刻，使四边形为菱形，若存在，求的值；若不存在，请说明理由

Answer 1

【答案】(1)当时，四边形为平行四边形；(2)点到的距离；(3)存在，，使四边形为菱形.

【解析】

（1）先判断出四边形CNPD为矩形，然后根据四边形为平行四边形得，即可求出t值；

（2）设点到的距离，利用勾股定理先求出AC，然后根据面积不变求出点到的距离；

（3）由NP⊥AD，QP=PK，可得当PM=PA时有四边形AQMK为菱形，列出方程6-t-2t=8-（6-t），求解即可.

解：(1)根据题意可得，

∵在四边形ABCD中，AD∥BC，∠ADC=90°，NP⊥AD于点P，

∴四边形CNPD为矩形，

∴

∴

∵四边形为平行四边形，

，

∴

解得：，

∴当时，四边形为平行四边形；

(2)设点到的距离，

在中，

，

在中，

∴

∴点到的距离

(3)存在． 理由如下：

∵将沿翻折得

∵，

∴当时有四边形为菱形，

∴，

解得，

∴，使四边形为菱形.