题目内容
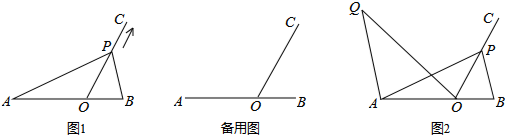
在△ABC中,AC=BC,∠ACB=120°,点D在AB边上,∠EDF=60°.
(1)当点D为AB中点时,且∠EDF的两边分别交线段AC、BC于点E、F,如图1,求证:DE=DF;
(2)当点D不是AB中点,且
=
时,
①若∠EDF的两边分别交线段AC、BC于点E、F,如图2,求
;
②若∠EDF的边DE交线段AC于点E,边DF交BC延长线于点F,如图3,直接写出
的值.

(1)当点D为AB中点时,且∠EDF的两边分别交线段AC、BC于点E、F,如图1,求证:DE=DF;
(2)当点D不是AB中点,且
| AD |
| AB |
| 1 |
| 3 |
①若∠EDF的两边分别交线段AC、BC于点E、F,如图2,求
| DE |
| DF |
②若∠EDF的边DE交线段AC于点E,边DF交BC延长线于点F,如图3,直接写出
| DE |
| DF |

考点:相似形综合题
专题:
分析:(1)根据等腰三角形的三线合一,可得CD平分∠ACB,根据角平分线的性质,可得DG与DH的关系,根据等角的补角相等,可得∠DFH=∠DEG,根据AAS,可得△DGE≌△DHF,根据全等三角形的性质,可得答案;
(2)根据两个角对应相等的两个三角形相似,可得△ADG∽△BDH,根据相似三角形的性质
=
=
,再根据相似三角形的判定与性质,可得答案;
(3)根据∠A=∠B,∠AGD=∠BHD,可得△ADG∽△BDH,根据相似三角形的性质,可得
=
=
,根据∠EDI=∠ICF,∠EID=∠FIC,∠EDI+∠EID+∠DEI=∠FIC+∠FCI+CFI=180°,可得∠DEG=∠DFH,根据两个角对应相等的两个三角形相似,可得△DEG∽△DFH,根据相似三角形的性质,可得答案.
(2)根据两个角对应相等的两个三角形相似,可得△ADG∽△BDH,根据相似三角形的性质
| DG |
| DH |
| AD |
| BD |
| 1 |
| 2 |
(3)根据∠A=∠B,∠AGD=∠BHD,可得△ADG∽△BDH,根据相似三角形的性质,可得
| DG |
| DH |
| AD |
| BD |
| 1 |
| 2 |
解答:解:(1)连接CD,过点D作DG⊥AC于点G,DH⊥BC于点H, ,
,
∴∠DGE=∠DHF=90°,
∵AC=BC,点D为AB中点,
∴CD平分∠ACB,
∴DG=DH.
∵∠ACB=120°,∠EDF=60°,
∴∠DEC+∠DFH=180°,
∵∠DEC+∠DEG=180°,
∴∠DFH=∠DEG,
在△DGE和△DHF中,
,
∴△DGE≌△DHF(AAS),
∴DE=DF
(2)①过点D作DG⊥AC于点G,DH⊥BC于点H, ,
,
∴∠DGE=∠DHF=∠DGA=∠DHC=90°.
∵AC=BC,
∴∠A=∠B,
∴△ADG∽△BDH,
∵
=
,
∴
=
=
,
 ∵∠DGE=∠DHF,∠DFH=∠DEG,
∵∠DGE=∠DHF,∠DFH=∠DEG,
∴△DGE∽△DHF,
∴
=
=
,
②如图3作DG⊥AC与G点,DH⊥BC与H点,
=
.
 ,
,∴∠DGE=∠DHF=90°,
∵AC=BC,点D为AB中点,
∴CD平分∠ACB,
∴DG=DH.
∵∠ACB=120°,∠EDF=60°,
∴∠DEC+∠DFH=180°,
∵∠DEC+∠DEG=180°,
∴∠DFH=∠DEG,
在△DGE和△DHF中,
|
∴△DGE≌△DHF(AAS),
∴DE=DF
(2)①过点D作DG⊥AC于点G,DH⊥BC于点H,
 ,
,∴∠DGE=∠DHF=∠DGA=∠DHC=90°.
∵AC=BC,
∴∠A=∠B,
∴△ADG∽△BDH,
∵
| AD |
| AB |
| 1 |
| 3 |
∴
| DG |
| DH |
| AD |
| BD |
| 1 |
| 2 |
 ∵∠DGE=∠DHF,∠DFH=∠DEG,
∵∠DGE=∠DHF,∠DFH=∠DEG,∴△DGE∽△DHF,
∴
| DE |
| DF |
| DG |
| DH |
| 1 |
| 2 |
②如图3作DG⊥AC与G点,DH⊥BC与H点,
| DE |
| DF |
| 1 |
| 2 |
点评:本题考查了相似形综合题,利用了等腰直角三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质.

练习册系列答案
相关题目
 如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为
如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为