题目内容
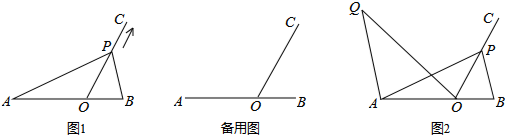
如图1,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.
(1)当t=
秒时,则OP= ,S△ABP= ;
(2)当△ABP是直角三角形时,求t的值;
(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求证:AQ•BP=3.
(1)当t=
| 1 |
| 2 |
(2)当△ABP是直角三角形时,求t的值;
(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求证:AQ•BP=3.

考点:相似形综合题
专题:几何动点问题,压轴题
分析:(1)如答图1所示,作辅助线,利用三角函数或勾股定理求解;
(2)当△ABP是直角三角形时,有三种情形,需要分类讨论;
(3)如答图4所示,作辅助线,构造一对相似三角形△OAQ∽△PBO,利用相似关系证明结论.
(2)当△ABP是直角三角形时,有三种情形,需要分类讨论;
(3)如答图4所示,作辅助线,构造一对相似三角形△OAQ∽△PBO,利用相似关系证明结论.
解答:(1)解:当t=
秒时,OP=2t=2×
=1.
如答图1,过点P作PD⊥AB于点D.

在Rt△POD中,PD=OP•sin60°=1×
=
,
∴S△ABP=
AB•PD=
×(2+1)×
=
.
(2)解:当△ABP是直角三角形时,
①若∠A=90°.
∵∠BOC=60°且∠BOC>∠A,
∴∠A≠90°,故此种情形不存在;
②若∠B=90°,如答图2所示:

∵∠BOC=60°,
∴∠BPO=30°,
∴OP=2OB=2,又OP=2t,
∴t=1;
③若∠APB=90°,如答图3所示:

过点P作PD⊥AB于点D,则OD=OP•sin30°=t,PD=OP•sin60°=
t,
∴AD=OA+OD=2+t,BD=OB-OD=1-t.
在Rt△ABP中,由勾股定理得:PA2+PB2=AB2
∴(AD2+PD2)+(BD2+PD2)=AB2,
即[(2+t)2+(
t)2]+[(1-t)2+(
t)2]=32
解方程得:t=
或t=
(负值舍去),
∴t=
.
综上所述,当△ABP是直角三角形时,t=1或t=
.
(3)证明:如答图4,过点O作OE∥AP,交PB于点E,
则有
=
=
,
∴PE=
PB.

∵AP=AB,
∴∠APB=∠B,
∵OE∥AP,
∴∠OEB=∠APB,
∴∠OEB=∠B,
∴OE=OB=1,∠3+∠B=180°.
∵AQ∥PB,
∴∠OAQ+∠B=180°,
∴∠OAQ=∠3;
∵∠AOP=∠1+∠QOP=∠2+∠B,∠QOP=∠B,
∴∠1=∠2;
∴△OAQ∽△PEO,
∴
=
,即
=
,
化简得:AQ•PB=3.
| 1 |
| 2 |
| 1 |
| 2 |
如答图1,过点P作PD⊥AB于点D.

在Rt△POD中,PD=OP•sin60°=1×
| ||
| 2 |
| ||
| 2 |
∴S△ABP=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
(2)解:当△ABP是直角三角形时,
①若∠A=90°.
∵∠BOC=60°且∠BOC>∠A,
∴∠A≠90°,故此种情形不存在;
②若∠B=90°,如答图2所示:

∵∠BOC=60°,
∴∠BPO=30°,
∴OP=2OB=2,又OP=2t,
∴t=1;
③若∠APB=90°,如答图3所示:

过点P作PD⊥AB于点D,则OD=OP•sin30°=t,PD=OP•sin60°=
| 3 |
∴AD=OA+OD=2+t,BD=OB-OD=1-t.
在Rt△ABP中,由勾股定理得:PA2+PB2=AB2
∴(AD2+PD2)+(BD2+PD2)=AB2,
即[(2+t)2+(
| 3 |
| 3 |
解方程得:t=
-1+
| ||
| 8 |
-1-
| ||
| 8 |
∴t=
-1+
| ||
| 8 |
综上所述,当△ABP是直角三角形时,t=1或t=
-1+
| ||
| 8 |
(3)证明:如答图4,过点O作OE∥AP,交PB于点E,
则有
| BE |
| PE |
| OB |
| OA |
| 1 |
| 2 |
∴PE=
| 2 |
| 3 |

∵AP=AB,
∴∠APB=∠B,
∵OE∥AP,
∴∠OEB=∠APB,
∴∠OEB=∠B,
∴OE=OB=1,∠3+∠B=180°.
∵AQ∥PB,
∴∠OAQ+∠B=180°,
∴∠OAQ=∠3;
∵∠AOP=∠1+∠QOP=∠2+∠B,∠QOP=∠B,
∴∠1=∠2;
∴△OAQ∽△PEO,
∴
| AQ |
| OE |
| OA |
| PE |
| AQ |
| 1 |
| 2 | ||
|
化简得:AQ•PB=3.
点评:本题是运动型综合题,考查了相似三角形的判定与性质、解直角三角形、勾股定理、一元二次方程等多个知识点.第(2)问中,解题关键在于分类讨论思想的运用;第(3)问中,解题关键是构造相似三角形,本问有多种解法,可探究尝试.

练习册系列答案
相关题目
一组数据1,3,6,1,2的众数和中位数分别是( )
| A、1,6 | B、1,1 |
| C、2,1 | D、1,2 |

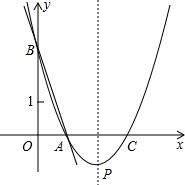 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与X轴交于另一点C,其顶点为P.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与X轴交于另一点C,其顶点为P.
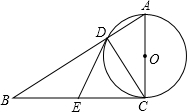 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.