题目内容
3. 如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10=75°.
如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10=75°.
分析 如图,作辅助线,首先证得$\widehat{{{{A}_{3}A}_{7}A}_{10}}$=$\frac{5}{12}$⊙O的周长,进而求得∠A3OA10=$\frac{5}{12}×360°$=150°,运用圆周角定理问题即可解决.
解答 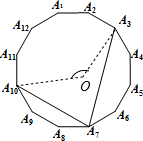 解:设该正十二边形的中心为O,如图,连接A10O和A3O,
解:设该正十二边形的中心为O,如图,连接A10O和A3O,
由题意知,$\widehat{{{{A}_{3}A}_{7}A}_{10}}$=$\frac{5}{12}$⊙O的周长,
∴∠A3OA10=$\frac{5}{12}×360°$=150°,
∴∠A3A7A10=75°,
故答案为:75°.
点评 此题主要考查了正多边形及其外接圆的性质及圆周角定理,作出恰当的辅助线,灵活运用有关定理来分析是解答此题的关键.

练习册系列答案
相关题目
9.sin60°的值等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
14.下列各组中的两个图形,不一定相似的是( )
| A. | 有一个角是120°的两个等腰三角形 | B. | 两个等边三角形 | ||
| C. | 两个直角三角形 | D. | 两个等腰直角三角形 |
15.已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a-b+c≥0;
④$\frac{a+b+c}{b-a}$的最小值为3.
其中,正确结论的个数为( )
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a-b+c≥0;
④$\frac{a+b+c}{b-a}$的最小值为3.
其中,正确结论的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为12、10、6、8,则第5组的频率是( )
| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.4 |
13.已知甲煤场有煤518吨,乙煤场有煤106吨,为了使甲煤场存煤是乙煤场的2倍,需要从甲煤场运煤到乙煤场,设从甲煤场运煤x吨到乙煤场,则可列方程为( )
| A. | 518=2(106+x) | B. | 518-x=2×106 | C. | 518-x=2(106+x) | D. | 518+x=2(106-x) |
 某农场拟建三间长方形种牛饲养室,饲养室的一面靠墙(墙长50m),中间用两道墙隔开(如图).已知计划中的建筑材料可建墙的总长度为48m,则这三间长方形种牛饲养室的总占地面积的最大值为144m2.
某农场拟建三间长方形种牛饲养室,饲养室的一面靠墙(墙长50m),中间用两道墙隔开(如图).已知计划中的建筑材料可建墙的总长度为48m,则这三间长方形种牛饲养室的总占地面积的最大值为144m2. 如图,大海中某灯塔P周围10海里范围内有暗礁,一艘海轮在点A处观察灯塔P在北偏东60°方向,该海轮向正东方向航行8海里到达点B处,这时观察灯塔P恰好在北偏东45°方向.如果海轮继续向正东方向航行,会有触礁的危险吗?试说明理由.(参考数据:$\sqrt{3}$≈1.73)
如图,大海中某灯塔P周围10海里范围内有暗礁,一艘海轮在点A处观察灯塔P在北偏东60°方向,该海轮向正东方向航行8海里到达点B处,这时观察灯塔P恰好在北偏东45°方向.如果海轮继续向正东方向航行,会有触礁的危险吗?试说明理由.(参考数据:$\sqrt{3}$≈1.73)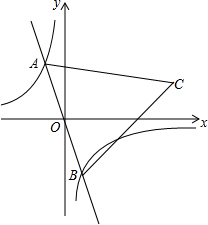 如图,在反比例函数y=-$\frac{2}{x}$的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=$\frac{k}{x}$的图象上运动.若tan∠CAB=2,则k的值为( )
如图,在反比例函数y=-$\frac{2}{x}$的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=$\frac{k}{x}$的图象上运动.若tan∠CAB=2,则k的值为( )