题目内容
如图，对于大于或等于2的自然数n的平方进行如下“分裂”，分裂成n个连续奇数的和，则自然数112的分裂数中最中间的数是 ，自然数n2的分裂数中最大的数是 ．
考点：规律型：数字的变化类
专题：
分析：根据前面分解的具体数值，发现：底数为奇数时分裂数有奇数个，其中最中间的数与底数相同，则自然数112的分裂数中最中间的数是11；而每个数中所分解的最大的数是底数的2倍减去1，则自然数n2的分裂数中最大的数是2n-1．
解答：解：根据题意可知
自然数112的分裂数中最中间的数是11；
自然数n2的分裂数中最大的数是2n-1．
故答案为：11，2n-1．
自然数112的分裂数中最中间的数是11；
自然数n2的分裂数中最大的数是2n-1．
故答案为：11，2n-1．
点评：此题主要考查学生对规律型题的掌握情况，注意根据具体的数值进行分析分解的最中间的数与最大的数和底数的规律，从而推广到一般．
练习册系列答案
相关题目
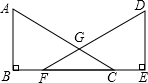已知：如图，点B，F，C，E在同一直线上，AC，DF相交于点G，AB⊥BE，垂足为B，DE⊥BE，垂足为E，且AC=DF，BF=CE．求证：∠ACB=∠DFE．
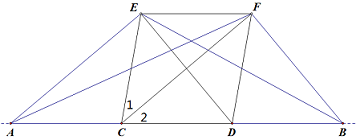如图，点C，D在线段AB上，EF∥AB，CE=CD，∠1=∠2．
如图，小明为了测量其所在位置A点到河对岸B点之间的距离，沿着与AB垂直的方向走了m米，到达点C，测得∠ACB=α，那么AB等于