题目内容
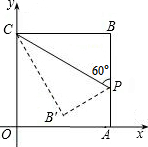 如图,平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,沿CP折叠正方形,折叠后的点B落在平面内的点B′处,已知直线CB′的解析式为y=-
如图,平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,沿CP折叠正方形,折叠后的点B落在平面内的点B′处,已知直线CB′的解析式为y=-| 3 |
考点:一次函数综合题
专题:
分析:作B'E⊥OC于点E,在直角△B'CE中,利用三角函数求得CE和B'E的长,从而求得B′的坐标,进而得到P的坐标,然后利用待定系数法求得直线CP的解析式.
解答: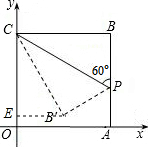 解:作B'E⊥OC于点E.
解:作B'E⊥OC于点E.
∵四边形OABC是正方形,点A的坐标是(4,0),
∴OA=BC=B'C=4,
又∵直角△BCP中,∠BPC=60°,
∴∠BCP=30°,
则∠B'CP=30°,∠B'CE=30°,
∴CE=B'C•cos30°=4×
=2
,B'E=BP=B'C•sin30°=4×
=2,
∴B'的坐标是(2,4-2
),P的坐标是(4,2).
设直线CP的解析式是y=kx+b,则
,
解得:
,
则直线的解析式是:y=-
x+4.
故答案是:(2,4-2
),y=-
x+4.
 解:作B'E⊥OC于点E.
解:作B'E⊥OC于点E.∵四边形OABC是正方形,点A的坐标是(4,0),
∴OA=BC=B'C=4,
又∵直角△BCP中,∠BPC=60°,
∴∠BCP=30°,
则∠B'CP=30°,∠B'CE=30°,
∴CE=B'C•cos30°=4×
| ||
| 2 |
| 3 |
| 1 |
| 2 |
∴B'的坐标是(2,4-2
| 3 |
设直线CP的解析式是y=kx+b,则
|
解得:
|
则直线的解析式是:y=-
| 1 |
| 2 |
故答案是:(2,4-2
| 3 |
| 1 |
| 2 |
点评:本题考查了图形的折叠和待定系数法求函数的解析式,正确求得B'的坐标是关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
如果x:y=2:3,则下列各式不成立的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

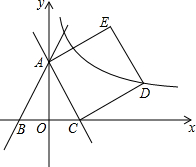 在平面直角坐标系中,直线y=2x+2分别与y轴,x轴交于点A,B两点,在x轴正半轴上取一点C,使OC=OB,以AC为边长在第一象限作正方形ACDE,顶点D恰好在反比例函数y=
在平面直角坐标系中,直线y=2x+2分别与y轴,x轴交于点A,B两点,在x轴正半轴上取一点C,使OC=OB,以AC为边长在第一象限作正方形ACDE,顶点D恰好在反比例函数y=
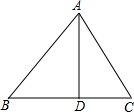 如图,在△ABC中,AD⊥BC,垂足为D.若AD=4,BC=7,∠B=45°,则AC边的长是
如图,在△ABC中,AD⊥BC,垂足为D.若AD=4,BC=7,∠B=45°,则AC边的长是