题目内容
12.$\sqrt{6}$+$\sqrt{8}$×$\sqrt{12}$=5$\sqrt{6}$;$\sqrt{(-2)^{2}}$-4$\sqrt{\frac{1}{2}}$=2-2$\sqrt{2}$.分析 先把各二次根式化为最简二次根式,得到$\sqrt{6}$+$\sqrt{8}$×$\sqrt{12}$=$\sqrt{6}$+2$\sqrt{2}$×2$\sqrt{3}$,然后进行二次根式的乘法运算后合并即可;根据二次根式的性质化简$\sqrt{(-2)^{2}}$-4$\sqrt{\frac{1}{2}}$即可.
解答 解:$\sqrt{6}$+$\sqrt{8}$×$\sqrt{12}$=$\sqrt{6}$+2$\sqrt{2}$×2$\sqrt{3}$=$\sqrt{6}$+4$\sqrt{6}$=5$\sqrt{6}$;
$\sqrt{(-2)^{2}}$-4$\sqrt{\frac{1}{2}}$=2-2$\sqrt{2}$.
故答案为5$\sqrt{6}$,2-2$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
2.一个学习兴趣小组有4名女生,6名男生,现要从这10名学生中选出一人担当组长,则女生当组长的概率是( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
 如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点A,在近岸取点D,B,使得A,D,B在一条直线上,且与河的边沿垂直,测得BD=10m,然后又在垂直AB的直线上取点C,并量得BC=30m.如果DE=20m,则河宽AD为20m.
如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点A,在近岸取点D,B,使得A,D,B在一条直线上,且与河的边沿垂直,测得BD=10m,然后又在垂直AB的直线上取点C,并量得BC=30m.如果DE=20m,则河宽AD为20m.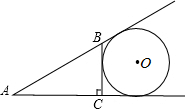 如图,在△ABC中,AB=5,BC=3,AC=4,⊙O与BC边及AB,AC的延长线相切,则⊙O的半径为2.
如图,在△ABC中,AB=5,BC=3,AC=4,⊙O与BC边及AB,AC的延长线相切,则⊙O的半径为2.