Question

20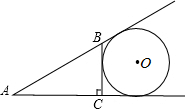．如图，在△ABC中，AB=5，BC=3，AC=4，⊙O与BC边及AB，AC的延长线相切，则⊙O的半径为2．

Answer 1

分析 先连接OD、OE，根据⊙O与△ABC中AB、AC的延长线及BC边相切，得出AF=AD，BE=BF，CE=CD，再根据OD⊥AD，OE⊥BC，∠ACB=90°，得出四边形ODCE是正方形，最后设OD=r，列出5+3-r=4+r，求出r=2即可．

解答 解：如图设切点分别为E、F、D，连接OD、OE，
∵⊙O与△ABC中AB、AC的延长线及BC边相切，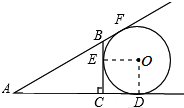
∴AF=AD，BE=BF，CE=CD，
OD⊥AD，OE⊥BC，
∵∠ACB=90°，
∴四边形ODCE是正方形，
设OD=r，则CD=CE=r，
∵BC=3，
∴BE=BF=3-r，
∵AB=5，AC=4，
∴AF=AB+BF=5+3-r，
AD=AC+CD=4+r，
∴5+3-r=4+r，
r=2，
则⊙O的半径是2．
故答案为：2．

点评 此题考查了切线长定理、正方形的性质、圆的性质等，解题的关键是设出圆的半径，列出关于圆的半径的方程，用方程的思想解决问题．