ƒøƒ⁄»›
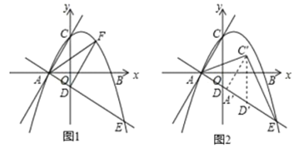
°æƒø°ø≈◊ŒÔœfly£Ω©Åx2+bx+c”Îx÷·Ωª”⁄A£¨B¡Ωµ„£®µ„A‘⁄B◊Û±fl£©£¨”Îy÷·Ωª”⁄µ„C£Æ
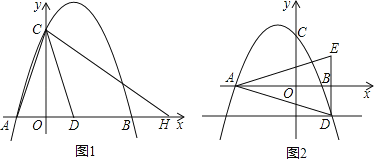
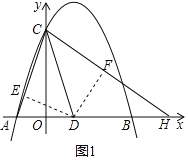
£®1£©»ÁÕº1£¨“—÷™A£®©Å1£¨0£©£¨B£®3£¨0£©£Æ
¢Ÿ÷±Ω”–¥≥ˆ≈◊ŒÔœflµƒΩ‚Œˆ Ω£ª
¢⁄µ„H‘⁄x÷·…œ£¨D£®1£¨0£©£¨¡¨Ω”AC£¨DC£¨HC£¨»ÙCD∆Ω∑÷°œACH£¨«Ûµ„Hµƒ◊¯±Í£ª
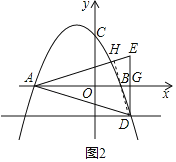
£®2£©»ÁÕº2£¨÷±œfly£Ω©Å1”Î≈◊ŒÔœfly£Ω©Åx2+bx+cΩª”⁄µ„D£¨µ„E£¨Dπÿ”⁄x÷·∂‘≥∆£Æ
¢Ÿ»Ùµ„D‘⁄≈◊ŒÔœfl∂‘≥∆÷·µƒ”“≤‡£¨«Û÷§£∫DB°ÕAE£ª
¢⁄»Ùµ„D‘⁄≈◊ŒÔœfl∂‘≥∆÷·µƒ◊Û≤‡£¨«Î÷±Ω”≈–∂œ£¨BD «∑Ò¥π÷±AE£ø
°æ¥∞∏°ø£®1£©¢Ÿy£Ω©Åx2+2x+3£ª¢⁄µ„Hµƒ◊¯±ÍŒ™£®![]() £¨0£©£ª£®2£©¢Ÿº˚Ω‚Œˆ£ª¢⁄DB°ÕAE
£¨0£©£ª£®2£©¢Ÿº˚Ω‚Œˆ£ª¢⁄DB°ÕAE
°æΩ‚Œˆ°ø
£®1£©¢Ÿ”√¥˝∂®œµ ˝∑®Ω‚¥±„ø…£ª
¢⁄π˝D◊˜DE°ÕAC”⁄µ„E£¨DF°ÕCH”⁄µ„F£¨«Û≥ˆDF£¨…ËH£®m£¨0£©£¨‘Ÿ”…»˝Ω«–Œµƒ√ʪ˝π´ Ω¡–≥ˆmµƒ∑Ω≥ÃΩ¯––Ω‚¥£ª
£®2£©¢Ÿ…ËDE”Îx÷·µƒΩªµ„Œ™Gµ„£¨¡¨Ω”DB£¨≤¢—”≥§DB”ÎAEΩª”⁄µ„H£¨‘À”√«Û∫Ø ˝ÕºœÛµƒΩªµ„◊¯±Íµƒ∑Ω∑®«Û≥ˆA°¢B£¨Dµ„◊¯±Í£¨«Ûµ√DG°¢BG°¢AG°¢EG£¨‘Ÿ÷§√˜°˜DBG°◊°˜AGE±„ø…µ√Ω·¬€£ª
¢⁄∑¬’’…œ√Ê∑Ω∑®±„ø…µ√Ω·¬€£Æ
Ω‚£∫£®1£©¢Ÿ∞—A£®©Å1£¨0£©£¨B£®3£¨0£©¥˙»Îy£Ω©Åx2+bx+c£¨µ√
![]() £¨
£¨
°‡![]() £¨
£¨
°‡≈◊ŒÔœflµƒΩ‚Œˆ ΩŒ™£∫y£Ω©Åx2+2x+3£ª
¢⁄π˝D◊˜DE°ÕAC”⁄µ„E£¨DF°ÕCH”⁄µ„F£¨»ÁÕº1£¨
°fly£Ω©Åx2+2x+3
°‡C£®0£¨3£©£¨
°‡OC£Ω3£¨
°flA£®©Å1£¨0£©£¨B£®3£¨0£©£¨D£®1£¨0£©£¨
°‡OA£Ω1£¨OB£Ω3£¨OD£Ω1£¨AD£Ω2£¨
°‡![]() £¨
£¨
°fl![]() £¨
£¨
°‡![]() £¨
£¨
°flCD∆Ω∑÷°œACH£¨
°‡![]() £¨
£¨
…˵„Hµƒ◊¯±ÍŒ™£®m£¨0£©£¨‘ÚDH£Ωm©Å1£¨![]() £¨
£¨
°fl![]() £¨
£¨
°‡![]() £¨
£¨
°‡m£Ω©Å1£®…·»•£©£¨ªÚ![]() £¨
£¨
°‡µ„Hµƒ◊¯±ÍŒ™£®![]() £¨0£©£ª
£¨0£©£ª
£®2£©¢Ÿ…ËDE”Îx÷·µƒΩªµ„Œ™Gµ„£¨¡¨Ω”DB£¨≤¢—”≥§DB”ÎAEΩª”⁄µ„H£¨»ÁÕº2£¨
°fl≈◊ŒÔœfly£Ω©Åx2+bx+c”Îx÷·Ωª”⁄A£¨B¡Ωµ„£®µ„A‘⁄B◊Û±fl£©£¨
°‡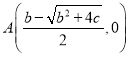 £¨
£¨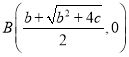 £¨
£¨
°fl÷±œfly£Ω©Å1”Î≈◊ŒÔœfly£Ω©Åx2+bx+cΩª”⁄µ„D£¨µ„D‘⁄≈◊ŒÔœfl∂‘≥∆÷·µƒ”“≤‡£¨
°‡Dµ„µƒ◊¯±ÍŒ™ £¨
£¨
°flµ„E£¨Dπÿ”⁄x÷·∂‘≥∆£¨
°‡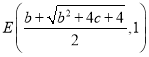 £¨DG£ΩEG£Ω1£¨
£¨DG£ΩEG£Ω1£¨
°‡![]() £¨
£¨
![]()
°‡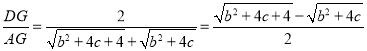 £¨
£¨![]() £¨
£¨
°‡![]() £¨
£¨
°fl°œDGB£Ω°œAGE£Ω90°„£¨
°‡°˜DGB°◊°˜AGE£¨
°‡°œBDG£Ω°œEAG£¨
°fl°œEAG+°œAEG£Ω90°„£¨
°‡°œBDG+°œAEG£Ω90°„£¨
°‡°œDHE£Ω90°„£¨
°‡DB°ÕAE£ª
¢⁄BD°ÕAE£Æ»ÁÕº3£¨
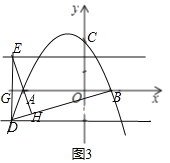
°fl≈◊ŒÔœfly£Ω©Åx2+bx+c”Îx÷·Ωª”⁄A£¨B¡Ωµ„£®µ„A‘⁄B◊Û±fl£©£¨
°‡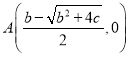 £¨
£¨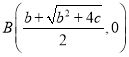 £¨
£¨
°fl÷±œfly£Ω©Å1”Î≈◊ŒÔœfly£Ω©Åx2+bx+cΩª”⁄µ„D£¨µ„D‘⁄≈◊ŒÔœfl∂‘≥∆÷·µƒ◊Û≤‡£¨
°‡Dµ„µƒ◊¯±ÍŒ™ £¨
£¨
°flµ„E£¨Dπÿ”⁄x÷·∂‘≥∆£¨
°‡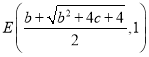 £¨DG£ΩEG£Ω1£¨
£¨DG£ΩEG£Ω1£¨
°‡![]() £¨
£¨
![]() £¨
£¨
°‡![]() £¨
£¨
°fl°œDGB£Ω°œAGF£Ω90°„£¨
°‡°˜DGB°◊°˜AGE£¨
°‡°œBDG£Ω°œEAG£¨
°fl°œEAG+°œAEG£Ω90°„£¨
°‡°œBDG+°œAEG£Ω90°„£¨
°‡°œDHE£Ω90°„£¨
°‡DB°ÕAE£Æ
π ¥∞∏ «£∫£®1£©¢Ÿy£Ω©Åx2+2x+3£ª¢⁄µ„Hµƒ◊¯±ÍŒ™£®![]() £¨0£©£ª£®2£©¢Ÿº˚Ω‚Œˆ£ª¢⁄DB°ÕAE
£¨0£©£ª£®2£©¢Ÿº˚Ω‚Œˆ£ª¢⁄DB°ÕAE