题目内容
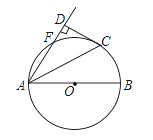
【题目】如图,AB是⊙O的直径,点F、C在⊙O上且![]() , 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
, 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
(1)求证:CD是⊙O的切线;
(2)若![]() , CD=4,求⊙O的半径.
, CD=4,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连结OC,由![]() ,根据圆周角定理得∠FAC=∠BAC,而∠OAC=∠OCA,则∠FAC=∠OCA,可判断OC∥AF,由于CD⊥AF,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
,根据圆周角定理得∠FAC=∠BAC,而∠OAC=∠OCA,则∠FAC=∠OCA,可判断OC∥AF,由于CD⊥AF,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
(2)连结BC,由AB为直径得∠ACB=90°,由F,C,B三等分半圆得∠BOC=60°,则∠BAC=30°,所以∠DAC=30°,在Rt△ADC中,利用含30度的直角三角形三边的关系得AC=2CD=8,在Rt△ACB中,根据勾股定理求得AB,进而求得⊙O的半径.
(1)证明:连结OC,如图,
∵![]() ,
,
∴∠FAC=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠FAC=∠OCA,
∴OC∥AF,
∵CD⊥AF,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:连结BC,如图,
∵AB为直径,
∴∠ACB=90°,
∵![]() =
=![]() ,
,
∴∠BOC=![]() ×180°=60°,
×180°=60°,
∴∠BAC=30°,
∴∠DAC=30°,
在Rt△ADC中,CD=4,
∴AC=2CD=8,
在Rt△ACB中,BC2+AC2=AB2 ,
即82+(![]() AB)2=AB2 ,
AB)2=AB2 ,
∴AB=![]() ,
,
∴⊙O的半径为![]() .
.

【题目】为了解市民对“雾霾天气的主要原因”的认识,某调查公司随机抽查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.
组别 | 观点 | 频数(人数) |
| 大气气压低,空气不流动 | 100 |
| 底面灰尘大,空气湿度低 |
|
| 汽车尾气排放 |
|
| 工厂造成的污染 | 140 |
| 其他 | 80 |
调查结果扇形统计图

请根据图表中提供的信息解答下列问题:
(1)填空:![]() __________,
__________,![]() __________.扇形统计图中
__________.扇形统计图中![]() 组所占的百分比为__________%.
组所占的百分比为__________%.
(2)若该市人口约有100万人,请你估计其中持![]() 组“观点”的市民人数约是__________万人.
组“观点”的市民人数约是__________万人.
(3![]() 组“观点”的概率是__________.
组“观点”的概率是__________.