Question

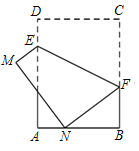
【题目】如图，在矩形的边上取一点将沿折叠，顶点正好落在边的中点上，设．

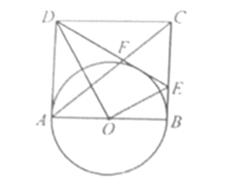
（1）直接写出的值和的度数；

（2）求证：直线是以为直径的的切线；

（3）连接交于点求的边上的高．

Answer 1

【答案】（1）；（2）见详解；（3）

【解析】

(1)由折叠和圆的性质直接可求；

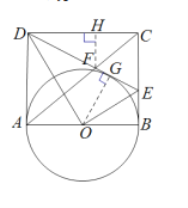
(2)作OG⊥DE于点G，证明△ADO≌△GDO(AAS)即可；

(3)作FH⊥CD于点H，证明△CEF∽△ADF，则有，再证明△CFH∽△CAD，即可求FH=.

解：∵O是AB的中点，
∴OA=OB= AB= ×6=3，
由折叠可得：CD=OD，∠CDE=∠ODE，CE=OE，
∵矩形ABCD，
∴CD=AB=6，BC=AD，∠DAB=∠ABC=90°，
∴OD=6，
∴∠ADO=30°，y=AD=3，
∴BC=3，
在Rt△OBE中，由勾股定理，得
(3x)2=32+x2，
解得：x=．
故答案为x=，y=3，∠ADO=30°；

证明：作于点

由折叠得

又

．

直线是的切线．

解：作于点

，即

即的边上的高为