题目内容
12.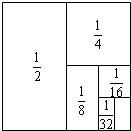 如图:把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的正方形,接着把其中一个面积为$\frac{1}{2}$的正方形等分成两个面积为$\frac{1}{4}$的正方形,再把其中一个面积为$\frac{1}{4}$的正方形等分成两个面积为$\frac{1}{8}$的正方形,如此进行下去,试观察图形来计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{256}$.
如图:把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的正方形,接着把其中一个面积为$\frac{1}{2}$的正方形等分成两个面积为$\frac{1}{4}$的正方形,再把其中一个面积为$\frac{1}{4}$的正方形等分成两个面积为$\frac{1}{8}$的正方形,如此进行下去,试观察图形来计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{256}$.
分析 根据图形揭示的规律,把一个面积为1的正方形分8次得到的面积为$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{256}$=1-$\frac{1}{256}$=$\frac{255}{256}$.
解答 解:根据题意得:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{256}$
=1-$\frac{1}{256}$
=$\frac{255}{256}$.
点评 本题考查了规律型:数字的变化类:认真观察、仔细思考,得出规律是解决这类问题的方法.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
7.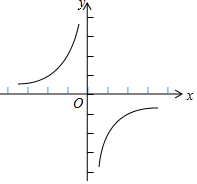 如图,图象对应的函数表达式为( )
如图,图象对应的函数表达式为( )
 如图,图象对应的函数表达式为( )
如图,图象对应的函数表达式为( )| A. | y=5x | B. | $y=\frac{2}{x}$ | C. | $y=\frac{1}{x}$ | D. | $y=-\frac{2}{x}$ |
17.2008年在北京举办了第29届夏季奥运会,观察如表
若用n表示奥运会届数,试用含n的代数式表示相应的举办年份是4n+1892.
| 届数 | 第1届 | 第2届 | 第3届 | … | 第29届 | … |
| 举办年份 | 1896年 | 1900年 | 1904年 | 2008年 |
1.若x<y成立,则下列不等式成立的是( )
| A. | x+1>y+1 | B. | x-2<y-2 | C. | -x<-y | D. | -3x<-3y |
2.下列各式中计算正确的是( )
| A. | x5+x4=x9 | B. | x2•x3=x5 | C. | x3+x3=x6 | D. | (-x2)3=-x5 |
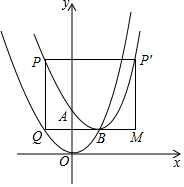 如图,在平面直角坐标系中,抛物线y=a(x-2)2+2经过点A(0,4),与其对称轴交于点B,P为抛物线y=a(x-2)2+2上一点,过点P分别作x轴、y轴的垂线,交抛物线y=a(x-h)2+h于点Q,交抛物线y=a(x-2)2+2于点P′,以PQ、PP′为邻边作矩形PP′MQ,设点P的横坐标为m(m≤0).
如图,在平面直角坐标系中,抛物线y=a(x-2)2+2经过点A(0,4),与其对称轴交于点B,P为抛物线y=a(x-2)2+2上一点,过点P分别作x轴、y轴的垂线,交抛物线y=a(x-h)2+h于点Q,交抛物线y=a(x-2)2+2于点P′,以PQ、PP′为邻边作矩形PP′MQ,设点P的横坐标为m(m≤0).