题目内容
14.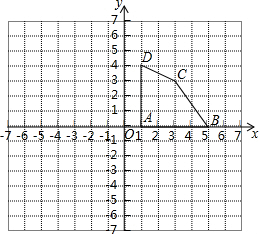 如图,四边形ABCD各顶点的坐标分别为A(1,0),B(5,0),C(3,3),D(1,4).将四边形ABCD先向下平移4个单位长度,再向左平移6个单位长度,得到四边形A′B′C′D′.
如图,四边形ABCD各顶点的坐标分别为A(1,0),B(5,0),C(3,3),D(1,4).将四边形ABCD先向下平移4个单位长度,再向左平移6个单位长度,得到四边形A′B′C′D′.(1)在图中画出四边形A′B′C′D′,并写出点A的对应点A′的坐标;
(2)如果将四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的,请指出这一平移方向和平移距离.
分析 (1)根据图形平移的性质画出四边形A′B′C′D′,并写出点A的对应点A′的坐标即可;
(2)连接AA′,利用勾股定理求出AA′的长度即可.
解答  解:(1)如图,四边形A′B′C′D′即为所求,A′(-5,-4);
解:(1)如图,四边形A′B′C′D′即为所求,A′(-5,-4);
(2)∵连接AA′,则AA′=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$,
∴平移的方向是由A到A′的方向,平移的距离是2$\sqrt{13}$个单位长度.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
相关题目
2.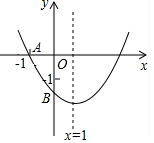 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc<0;②9a+3b+c=0;③4ac-b2<2a;④2b=3a.
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc<0;②9a+3b+c=0;③4ac-b2<2a;④2b=3a.
其中正确的结论是( )
 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc<0;②9a+3b+c=0;③4ac-b2<2a;④2b=3a.
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc<0;②9a+3b+c=0;③4ac-b2<2a;④2b=3a.其中正确的结论是( )
| A. | ①③ | B. | ②④ | C. | ①④ | D. | ②③ |
9.不等式x+1<8的最大整数解为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
4.如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,每旋转60°为滚动1次,那么当正六边形ABCDEF滚动2017次时,点F的坐标是( )


| A. | (2017,0) | B. | (2017$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | C. | (2018,$\sqrt{3}$) | D. | (2018,0) |
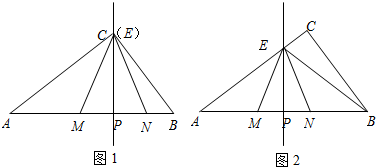
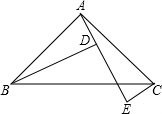 如图,A、D、E三点在同一直线上,且△BAD≌△ACE,∠ABD=30°,∠ADB=80°.
如图,A、D、E三点在同一直线上,且△BAD≌△ACE,∠ABD=30°,∠ADB=80°.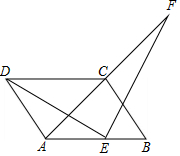 如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.
如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.