题目内容
18.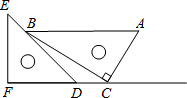 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,求BC、CD的长.
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,求BC、CD的长.
分析 过点B作BH⊥CF于H,如图,在Rt△ABC中利用∠A的正切定义可计算出BC=10$\sqrt{3}$,由于AB∥CF,则根据平行线的性质得到∠BCH=∠ABC=30°,则在Rt△BCH中利用含30度的直角三角形三边的关系得到BH=$\frac{1}{2}$BC=5$\sqrt{3}$,CH=$\sqrt{3}$BH=15,然后在Rt△BDH中,利用∠BDH=45°易得BH=DH=5$\sqrt{3}$,最后利用CD=CH-DH进行计算即可.
解答  解:过点B作BH⊥CF于H,如图,
解:过点B作BH⊥CF于H,如图,
在Rt△ABC中,∵tanA=$\frac{BC}{AC}$,
∴BC=10tan60°=10$\sqrt{3}$,
∵AB∥CF,
∴∠BCH=∠ABC=90°-∠A=30°,
在Rt△BCH中,∵∠BCH=30°,
∴BH=$\frac{1}{2}$BC=5$\sqrt{3}$,
CH=$\sqrt{3}$BH=15,
∵∠F=90°,∠E=45°,
∴∠EDF=45°,
在Rt△BDH中,∵∠BDH=45°,
∴BH=DH=5$\sqrt{3}$,
∴CD=CH-DH=15-5$\sqrt{3}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解直角三角形要用到的关系:锐角直角的关系:∠A+∠B=90°;三边之间的关系:a2+b2=c2;边角之间的关系:锐角三角函数关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.下列各式从左边到右边的变形是因式分解的是( )
| A. | x2+2x+1=x(x+2)+1 | B. | a2-6a+9=(a-3)2 | ||
| C. | (a+1)(a-1)=a2-1 | D. | -18x4y3=-6x2y2•3x2 |
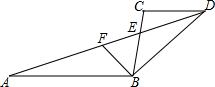 如图,已知AB∥CD,AD与BC相交于点E,BF平分∠ABC交AD于F.
如图,已知AB∥CD,AD与BC相交于点E,BF平分∠ABC交AD于F. 如图,已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.已知点E与点B关于AC对称,点E与点F关于BD对称.
如图,已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.已知点E与点B关于AC对称,点E与点F关于BD对称. 如图,在等腰直角△ABC中,∠ACB=90°,点O为斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:
如图,在等腰直角△ABC中,∠ACB=90°,点O为斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论: