题目内容
8. 如图,在正方形ABCD中,G是BC上任意一点,连接AG,DE⊥AG于E,BF∥DE交AG于F,探究线段AF、BF、EF三者之间的数量关系,并说明理由.
如图,在正方形ABCD中,G是BC上任意一点,连接AG,DE⊥AG于E,BF∥DE交AG于F,探究线段AF、BF、EF三者之间的数量关系,并说明理由.
分析 根据正方形的性质,可得AB=AD,∠DAB=∠ABC=90°,根据余角的性质,可得∠ADE=∠BAF,根据全等三角形的判定与性质,可得BF与AE的关系,再根据等量代换,可得答案.
解答 解:线段AF、BF、EF三者之间的数量关系AF=BF+EF,理由如下:
∵四边形ABCD是正方形,
∴AB=AD,∠DAB=∠ABC=90°.
∵DE⊥AG于E,BF∥DE交AG于F,
∴∠AED=∠DEF=∠AFB=90°,
∴∠ADE+∠DAE=90°,∠DAE+∠BAF=90°,
∴∠ADE=∠BAF.
在△ABF和△DAE中$\left\{\begin{array}{l}{∠BAF=∠ADE}\\{∠AFB=∠DEA}\\{AB=AD}\end{array}\right.$,
∴△ABF≌△DAE (AAS),
∴BF=AE.
∵AF=AE+EF,
AF=BF+EF.
点评 本题考查了全等三角形的判定与性质,利用了正方形的性质,余角的性质,全等三角形的判定与性质,等量代换.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.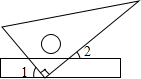 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=( )
如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=( )
 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=( )
如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=( )| A. | 52° | B. | 38° | C. | 42° | D. | 60° |
13.下列图形中,是轴对称图形,但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.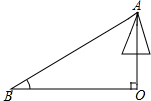 如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
 如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )| A. | $\frac{30}{tanα}$米 | B. | 30sinα米 | C. | 30tanα米 | D. | 30cosα米 |
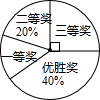 国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题: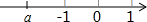 实数a在数轴的位置如图所示,则|a-1|=1-a.
实数a在数轴的位置如图所示,则|a-1|=1-a.