题目内容
13.化简后求值:已知a=2-$\sqrt{2}$,b=2+$\sqrt{2}$,求$\frac{{a}^{3}b+{a}^{2}{b}^{2}}{{a}^{2}+2ab+{b}^{2}}$$÷\frac{{a}^{2}-ab}{{a}^{2}-{b}^{2}}$的值.分析 先将分子、分母因式分解,同时可将除法转化为乘法,再约分计算分式的乘法可化简原式,将a、b的值代入计算可得答案.
解答 解:原式=$\frac{{a}^{2}b(a+b)}{(a+b)^{2}}$•$\frac{(a+b)(a-b)}{a(a-b)}$
=$\frac{{a}^{2}b}{a+b}$•$\frac{a+b}{a}$
=ab,
当a=2-$\sqrt{2}$,b=2+$\sqrt{2}$时,
原式=(2-$\sqrt{2}$)(2+$\sqrt{2}$)
=4-2
=2.
点评 本题主要考查分式的化简求值能力,熟练掌握分式的性质及分式运算法则是解题的关键.

练习册系列答案
相关题目
2.如果一个物体有七个顶点七个面,那么这个物体一定是( )
| A. | 五棱锥 | B. | 五棱柱 | C. | 六棱锥 | D. | 七棱锥 |
 、
、 在数轴上的位置,化简
在数轴上的位置,化简  .
.
 如图,点M在∠AOB的边OB上.
如图,点M在∠AOB的边OB上.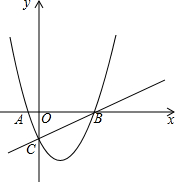 已知:抛物线y=x2+2mx+m,m为常数.
已知:抛物线y=x2+2mx+m,m为常数.