Question

7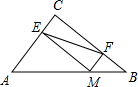．如图，在△ABC中，AC=9，BC=12，AB=15，点M为AB边上的点，过M作ME⊥AC交AC于E，MF⊥BC交BC于F，连接EF，则EF的最小值为$\frac{36}{5}$．

Answer 1

分析 连接CM，先根据勾股定理的逆定理得到∠ACB=90°，根据矩形的性质可知：EF=CM，当CM最小时，则EF最小，根据垂线段最短可知当CM⊥AB时，则EF最小，再根据三角形的面积即可求出EF的长．

解答 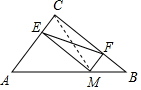解：连接CM，
在△ABC中，AC=9，BC=12，AB=15，
∵9²+12²=15²，
∴△ABC是直角三角形，
∴∠ACB=90°，
∵ME⊥AC，MF⊥BC，
∴四边形ECFM是矩形，
∴EF=CM，
当CM最小时，则EF最小，根据垂线段最短可知当CM⊥AB时，则CM最小，
∴EF=CM=$\frac{9×12}{15}$=$\frac{36}{5}$．
故答案为：$\frac{36}{5}$．

点评 本题考查了勾股定理的逆定理，矩形的判定和性质以及直角三角形的面积的不同求法，题目难度不大，设计很新颖，解题的关键是求EF的最小值转化为其相等线段CM的最小值．