题目内容
1.为了鼓励城区居民节约用水,某市规定用水收费标准如下:| 每户居民一个月用水量的范围 | 水费价格(范围:元/立方米) |
| 不超过20立方米 | a |
| 超过20立方米 | 不超过部分仍为a元,超过部分为b元 |
(1)求a,b的值;
(2)当用户居民月用水量为x立方米时,请用含x的式子表示应付水费;
(3)若估计该用户2015年一月份的水费支出大概是65±1元,求该用户该月份的用水量x的可能整数值.
分析 (1)根据某用户十一份用水15立方米,交水费22.5元,十二月份用水30立方米,交水费50元,分别求出a和b即可;
(2)分两段列出应付水费的关系式;
(3)根据“该用户2015年一月份的水费支出大概是65±1”列一元一次不等式组求解即可.
解答 解:(1)根据题意得:a=22.5÷15=1.5;
b=(50-20×1.5)÷(30-20)=2;
(2)当x≤20时,应付水费为ax=$\frac{3}{2}$x,
当x>20时,应付水费为20×1.5+(x-20)×2=2x-10;
(3)根据题意列不等式组得:60-1≤20×1.5+2(x-20)≤60+1,
解得:34.5≤x≤35.5,
∴该用户2015年一月份的用水量x的取值范围为34.5≤x≤35.5,
即:该用户该月份的用水量x的可能整数值是35立方米.
点评 此题是一元一次方程的应用,主要考查一元一次方程和一元一次不等式组的实际应用,难度适中,解题关键是根据题意准确列出不等式组.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
12.若$\left\{\begin{array}{l}x=-1\\ y=1\end{array}\right.$是方程组$\left\{\begin{array}{l}x+ay=0\\ bx+y=1\end{array}\right.$的解,则a、b的值为( )
| A. | a=0,b=1 | B. | a=1,b=0 | C. | a=0,b=0 | D. | a=1,b=1 |
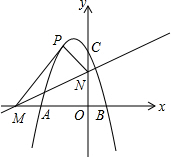 如图,抛物线y=-x2-2x+3与x轴交于A,B两点,与x轴交于C点,直线y=$\frac{1}{2}$x+m交x轴于M,交y轴于N,将△MON沿直线MN折叠,得到△MPN,若点P恰好落在第一象限的抛物线上,求点P的坐标及m的值.
如图,抛物线y=-x2-2x+3与x轴交于A,B两点,与x轴交于C点,直线y=$\frac{1}{2}$x+m交x轴于M,交y轴于N,将△MON沿直线MN折叠,得到△MPN,若点P恰好落在第一象限的抛物线上,求点P的坐标及m的值.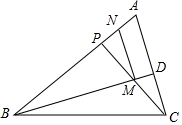 如图,已知在△ABC中,P为边AB上一点,连接CP,M为CP的中点,连接BM并延长,交AC于点D,N为AP的中点,连接MN.若∠ACP=∠ABD.
如图,已知在△ABC中,P为边AB上一点,连接CP,M为CP的中点,连接BM并延长,交AC于点D,N为AP的中点,连接MN.若∠ACP=∠ABD.