题目内容
2.化简:(1)$\frac{10\sqrt{3}}{\sqrt{50}}$;
(2)$\sqrt{\frac{n}{18m}}$(m>0,n≥0)
(3)4$\sqrt{\frac{3}{8}}$.
分析 (1)先化简二次根式,然后分子分母同时乘以$\sqrt{2}$即可;
(2)先分子分母同时乘以2m,然后再利用二次根式的性质化简即可;
(3)先分子分母同时乘以2,然后再利用二次根式的性质化简即可.
解答 解:(1)原式=$\frac{10\sqrt{3}}{5\sqrt{2}}$=2$\sqrt{6}$;
(2)原式=$\sqrt{\frac{2mn}{36{m}^{2}}}$=$\frac{\sqrt{2mn}}{6m}$;
(3)原式=4$\sqrt{\frac{6}{16}}$=4×$\frac{\sqrt{6}}{4}$=$\sqrt{6}$.
点评 本题主要考查的是分式的化简与计算,熟练掌握二次根式的性质是解题的关键.

练习册系列答案
相关题目
8.已知点A(3,-2)、B(1,-2),则直线AB( )
| A. | 与x轴垂直 | B. | 与x轴平行 | C. | 与y轴重合 | D. | 与x、y轴相交 |
6.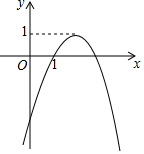 在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,则下列结论正确的是( )
在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,则下列结论正确的是( )
 在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,则下列结论正确的是( )
在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,则下列结论正确的是( )| A. | a<0,b<0,c>0 | |
| B. | -$\frac{b}{2a}$=1 | |
| C. | a+b+c<0 | |
| D. | 关于x的方程ax2+bx+c=-1有两个不相等的实数根 |
12.方程x2-6x+4=0的根的情况是( )
| A. | 没有实数根 | B. | 只有一个实数根 | ||
| C. | 有两个相等的实数根 | D. | 有两个不相等的实数根 |
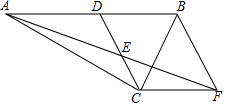 已知:如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,点E是CD的中点,过点C作CF∥AB交AE的延长线于点F.
已知:如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,点E是CD的中点,过点C作CF∥AB交AE的延长线于点F.