题目内容
8.已知二次函数y=ax2+bx-$\frac{5}{2}$的图象的顶点在直线y=2上,且图象过点(-5,0),试求a,b的值.分析 由二次函数y=ax2+bx-$\frac{5}{2}$的图象的顶点在直线y=2上,得出-$\frac{{b}^{2}+10a}{4a}$=2,图象过点(-5,0),代入函数得出25a-5b-$\frac{5}{2}$=0,两者联立方程组求得答案即可.
解答 解:∵二次函数y=ax2+bx-$\frac{5}{2}$的图象的顶点在直线y=2上,
∴-$\frac{{b}^{2}+10a}{4a}$=2,①
∵图象过点(-5,0),
∴25a-5b-$\frac{5}{2}$=0,②
①②联立方程组解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=-3}\end{array}\right.$或$\left\{\begin{array}{l}{a=-\frac{1}{50}}\\{b=-\frac{3}{5}}\end{array}\right.$.
点评 此题考查二次函数的性质,方程组的实际运用,掌握顶点坐标公式是解决问题的关键.

练习册系列答案
相关题目
13.△ABC和△DEF分别满足下列条件,其中△ABC与△DEF不相似的是( )
| A. | ∠A=∠D=45°,∠C=26°,∠E=109° | |
| B. | AB=1,AC=1.5,BC=2,DE=8,DF=12,EF=16 | |
| C. | AB=a,BC=b,AC=c,DE=$\sqrt{a}$,EF=$\sqrt{b}$,DF=$\sqrt{c}$ | |
| D. | AB=AC,DE=DF,∠A=∠D=40° |

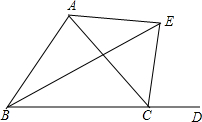 如图,点D是△ABC的边BC延长线上一点,BE平分∠ABC,CE平分∠ACD.求证:
如图,点D是△ABC的边BC延长线上一点,BE平分∠ABC,CE平分∠ACD.求证: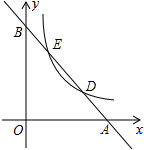 如图,已知直线l与x轴、y轴交于A、B两点,与双曲线y=$\frac{k}{x}$(k≠0,x>0)分别交于D、E两点,若点D坐标为(4,1),点E的坐标为(1,4).
如图,已知直线l与x轴、y轴交于A、B两点,与双曲线y=$\frac{k}{x}$(k≠0,x>0)分别交于D、E两点,若点D坐标为(4,1),点E的坐标为(1,4).