题目内容
17.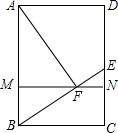 如图,已知矩形ABCD中,点E是CD边上的一点,连结BE,过点A作AF⊥BE.垂足为点F,且AF=BE,过点F作MN∥BC,与AB、CD边分别交于点M、N,求证:四边形AMND为正方形.
如图,已知矩形ABCD中,点E是CD边上的一点,连结BE,过点A作AF⊥BE.垂足为点F,且AF=BE,过点F作MN∥BC,与AB、CD边分别交于点M、N,求证:四边形AMND为正方形.
分析 由四边形ABCD是矩形,得到两组对边平行,四个角为直角,对角线相等,根据MN与BC平行,得到MN与AD平行,可得出四边形AMND是平行四边形,由一个角为直角的平行四边形是矩形得到AMND是矩形,得到∠AMN=90°,根据AF与BE垂直,得到一对直角相等,利用AAS得到三角形AFM与三角形BEC全等,利用全等三角形对应边相等得到AM=BC,根据AD=BC,得到AM=AD,利用邻边相等的矩形是正方形即可得证.
解答 证明:∵四边形ABCD是矩形,
∴AD∥BC,AB∥CD,∠BAD=∠C=∠ABC=90°,BC=AD,
∵MN∥BC,
∴MN∥AD,
又∵AB∥CD,
∴四边形AMND是平行四边形,
又∵∠BAD=90°,
∴四边形AMND是矩形,
∴∠AMN=90°,
∵AF⊥BE,
∴∠AFB=90°,
∵∠AFB+∠ABF+∠BAF=180°,
∴∠ABF+∠BAF=90°,
又∵∠ABC=∠ABF+∠EBC=90°,
∴∠BAF=∠EBC,
在△AFM和△BEC中,
$\left\{\begin{array}{l}{∠FAM=∠EBC}\\{∠AMF=∠C=90°}\\{AF=BE}\end{array}\right.$,
∴△AFM≌△BEC(AAS),
∴AM=BC,
又∵AD=BC,
∴AM=AD,
又∵四边形AMND是矩形,
∴四边形AMND是正方形.
点评 此题考查了正方形的判定,矩形的性质,全等三角形的判定与性质,熟练掌握正方形的判定方法是解本题的关键.

练习册系列答案
相关题目
8. 2016年里约热内卢奥运会(即第31届夏季奥林匹克运动会)开幕式将于当地时间8月5日在马拉卡纳体育场举行.如图是第31届夏季奥林匹克运动会会徽图案,下列关于它的对称性判定正确的是( )
2016年里约热内卢奥运会(即第31届夏季奥林匹克运动会)开幕式将于当地时间8月5日在马拉卡纳体育场举行.如图是第31届夏季奥林匹克运动会会徽图案,下列关于它的对称性判定正确的是( )
 2016年里约热内卢奥运会(即第31届夏季奥林匹克运动会)开幕式将于当地时间8月5日在马拉卡纳体育场举行.如图是第31届夏季奥林匹克运动会会徽图案,下列关于它的对称性判定正确的是( )
2016年里约热内卢奥运会(即第31届夏季奥林匹克运动会)开幕式将于当地时间8月5日在马拉卡纳体育场举行.如图是第31届夏季奥林匹克运动会会徽图案,下列关于它的对称性判定正确的是( )| A. | 只是轴对称图形 | |
| B. | 只是中心对称图形 | |
| C. | 既不是轴对称图形也不是中心对称图形 | |
| D. | 既是轴对称图形也是中心对称图形 |
 如图,在△ABC中,点D,E分别是边AB,BC的中点,若△DBE的周长是6,则△ABC的周长等于12.
如图,在△ABC中,点D,E分别是边AB,BC的中点,若△DBE的周长是6,则△ABC的周长等于12.
 如图,y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是x>2.
如图,y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是x>2.