题目内容
17. 已知:如图,?ABCD中,E,F两点在对角线BD上,BE=DF.
已知:如图,?ABCD中,E,F两点在对角线BD上,BE=DF.(1)求证:四边形AECF是平行四边形;
(2)当四边形AECF为矩形时,直接写出$\frac{BD-AC}{BE}$的值.
分析 (1)连接AC交BD于O,欲证明四边形AECF是平行四边形,只要证明OA=OC,OE=OF即可,
(2)根据矩形的性质AC=EF,得BD-AC=2BE,由此即可解决问题.
解答 (1)证明: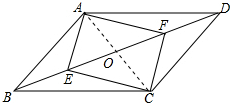 如图连接AC交BD于O,
如图连接AC交BD于O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=DF,
∴OA=OC,OE=OF,
∴四边形AECF是平行四边形.
(2)∵四边形AECF是矩形,
∴AC=EF
∴$\frac{BC-AC}{BE}$=$\frac{BE+EF+DF-AC}{BE}$=$\frac{2BE}{BE}$=2.
点评 本题考查平行四边形的性质、矩形的判定和性质,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
7.方程组$\left\{\begin{array}{l}{mx+2y=3}\\{x-3y=-4n}\end{array}\right.$有无数个解,则m、n的值为( )
| A. | m=$\frac{9}{8}$,n=-$\frac{2}{3}$ | B. | m=-$\frac{2}{3}$,n=$\frac{9}{8}$ | C. | m=$\frac{2}{3}$,n=-$\frac{9}{8}$ | D. | m=1,n=-$\frac{3}{4}$ |
12.下列标志既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.下列图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 任意写一个一元一次不等式,它的不等号的左、右两边都要有两项,且它的解集如图所示,这个不等式可以写成2x+2<x+1(答案不唯一).
任意写一个一元一次不等式,它的不等号的左、右两边都要有两项,且它的解集如图所示,这个不等式可以写成2x+2<x+1(答案不唯一).