题目内容
18. 如图在△ABC中,∠B=40°,∠C=60°,AD⊥BC于点D,AE平分∠BAC交BC于点E,DF⊥AE于点F.求∠ADF的度数.
如图在△ABC中,∠B=40°,∠C=60°,AD⊥BC于点D,AE平分∠BAC交BC于点E,DF⊥AE于点F.求∠ADF的度数.
分析 根据三角形内角和定理,可求得∠BAC的度数,由AE平分∠BAC,根据角平分线的定义,可求得∠CAE的度数,由AD⊥BC,根据直角三角形的性质,可求得∠CAD的度数,继而求得∠DAE的度数,则可求得∠ADF的度数.
解答 解:在△ABC中,∠B=40°,∠C=60°,
∴∠BAC=180°-∠B-∠C=80°,
∵AE平分∠BAC,
∴∠CAE=$\frac{1}{2}$∠BAC=40°,
∵AD⊥BC,
∴∠CAD=90°-∠C=30°,
∴∠DAE=∠CAE-∠CAD=10°,
∵DF⊥AE,
∴∠ADF=90°-∠DAE=80°.
点评 此题考查了三角形内角和定理与直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
7.芯片广泛用于计算机,电脑,手机等电子产品中,其物理效应运用了数学中的二进制原理,下表为二进制和二进制的换算原理,
则二进制1001101÷1011的结果是( )
| 十进制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| 二进制 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | … |
| A. | 1001 | B. | 111 | C. | 1101 | D. | 110 |
 如图,△ABC中,∠ACB=90°,∠CAB=45°,E是BC边上任意一点,过点C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
如图,△ABC中,∠ACB=90°,∠CAB=45°,E是BC边上任意一点,过点C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.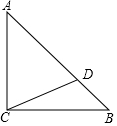 如图,在△ABC中,∠ACB=90°,AC=BC=AD
如图,在△ABC中,∠ACB=90°,AC=BC=AD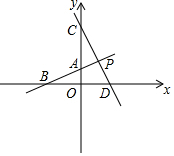 如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA:AC=2:5,直线CD垂直于直线AB于点P,交x轴于点D.
如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA:AC=2:5,直线CD垂直于直线AB于点P,交x轴于点D.