题目内容
16.(1)等腰三角形的周长为18,其中一边为5,则另两边的长分别为5cm、8cm或6.5cm、6.5cm.(2)等腰三角形一腰上的高与另一腰的夹角是28°,则顶角是62°或118°.
(3)在等腰Rt△ABC中,斜边上中线为5,则斜边长为10,面积是25.
分析 (1)分5cm是腰长与底边两种情况讨论求解即可;
(2)等腰三角形的高相对于三角形有三种位置关系,三角形内部,三角形的外部,三角形的边上.根据条件可知第三种高在三角形的边上这种情况不成立,因而可分两种情况进行讨论;
(3)根据直角三角形斜边上的中线等于斜边的一半即可求得斜边的长;再根据面积公式不难求得其面积.
解答 解:(1)①5cm是腰长时,底边=18-5×2=8cm,
所以,另两边长为5cm、8cm;
②5cm是底边时,腰长=∵$\frac{1}{2}$(18-5)=6.5cm,
所以,另两边长为6.5cm、6.5cm,
综上所述,另两边长为5cm、8cm或6.5cm、6.5cm.
故答案为:5cm、8cm或6.5cm、6.5cm;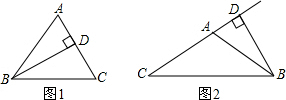 (2)分两种情况:
(2)分两种情况:
①当高在三角形内部时(如图1),
∵∠ABD=28°,
∴顶角∠A=90°-28°=62°;
②当高在三角形外部时(如图2),
∵∠ABD=28°,
∴顶角∠CAB=90°+28°=118°.
故答案为:62°或118°;
(3)∵在Rt△ABC中,斜边上的中线为5,
∴斜边=2×5=10,
故答案为:10;
∵△ABC是等腰直角三角形,斜边上的中线长为5,
∴斜边上的高线长为5,
则面积为$\frac{1}{2}×5×10$=25.
故答案为:25.
点评 此题主要考查了等腰三角形和直角三角形的性质以及三角形的面积计算.关键是掌握等腰三角形三线合一的性质和直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
7.已知a是有理数,下列各式:(-a)2=a2;-a2=(-a)2;(-a)3=a3;|-a3|=a3.其中一定成立的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.某生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组共互赠了180件,如果全组有x名学生,则根据题意列出的方程是( )
| A. | x(x+1)=182 | B. | x(x-1)=182 | C. | x(x-1)=182×2 | D. | x(x+1)=182×2 |
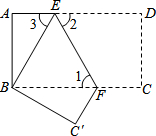 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.