题目内容
6．已知函数y=（2m-2）x+m+1（1）已知y随x增大而增大，求m的取值范围．
（2）图象过一、二、四象限，求m的取值范围．
分析 （1）据图象的增减性来确定（2m-2）的取值范围，从而求解；
（2）根据图象过一、二、四象限的特点解答即可．
解答 解：（1）∵一次函数y=（2m-2）x+m+1，若y随x的增大而增大，
∴2m-2＞0，
解得，m＞1．
（2）因为图象过一、二、四象限，可得：$\left\{\begin{array}{l}{2m-2＜0}\\{m+1＞0}\end{array}\right.$，
解得：-1＜m＜1．
点评 本题考查了一次函数的图象与系数的关系．
函数值y随x的增大而减小?k＜0；
函数值y随x的增大而增大?k＞0．
练习册系列答案
相关题目
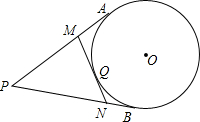如图，PA、PB是⊙O的切线，Q为$\widehat{AB}$上一点，过点Q的直线MN与⊙O相切，已知PA=4，则△PMN周长=8．
1．（-3）100×（$-\frac{1}{3}$）100等于（ ）
| A． | -3 | B． | 3 | C． | $\frac{1}{3}$ | D． | 1 |
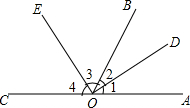∠AOB与∠BOC互为补角，OD平分∠AOB，∠3+∠2=90°，如图所示．求证∠BOE=$\frac{1}{2}$∠BOC．请完成下列证明．
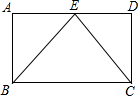如图所示，在?ABCD中，E为AD的中点，△CBE是等边三角形，求证：?ABCD是矩形．
15．下列分式的值，可以为零的是（ ）
| A． | $\frac{{x}^{2}+1}{x-1}$ | B． | $\frac{x+1}{{x}^{2}-1}$ | C． | $\frac{{x}^{2}+2x+1}{x+1}$ | D． | $\frac{x+1}{x-1}$ |