题目内容
17.若x+y=12,且x>0,y>0,则代数式$\sqrt{{x}^{2}+4}$+$\sqrt{{y}^{2}+9}$的最小值是13.分析 由x+y=12,得到y=12-x,于是得到原式=$\sqrt{{x}^{2}+4}$+$\sqrt{(12-x)^{2}+9}$=$\sqrt{(x-0)^{2}+(0-2)^{2}}$+$\sqrt{(x-12)^{2}+(0-3)^{2}}$,即可理解为x轴上的一点A(x,0)到B(0,2),C(12,3)的离的最小值,即AB+AC的最小值,如图,作B关于x轴的对称点B′,连接B′C,与x轴的交点即为点A,此时AB+AC的最小值为B′C的长度,根据两点间的距离公式即可求出B′C=$\sqrt{(12-0)^{2}+(3+2)^{2}}$=13.
解答 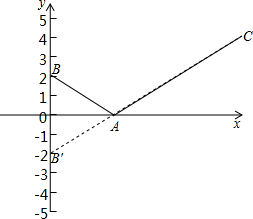 解:∵x+y=12,
解:∵x+y=12,
∴y=12-x,
∴原式=$\sqrt{{x}^{2}+4}$+$\sqrt{(12-x)^{2}+9}$=$\sqrt{(x-0)^{2}+(0-2)^{2}}$+$\sqrt{(x-12)^{2}+(0-3)^{2}}$,即可理解为x轴上的一点A(x,0)到B(0,2),C(12,3)的距离的最小值,即AB+AC的最小值,
如图,作B关于x轴的对称点B′,连接B′C,与x轴的交点即为点A,此时AB+AC的最小值为B′C的长度,
∵B(0,2),
∴B′(0,-2),
∴B′C=$\sqrt{(12-0)^{2}+(3+2)^{2}}$=13,
∴$\sqrt{{x}^{2}+4}$+$\sqrt{{y}^{2}+9}$的最小值为13,
故答案为:13.
点评 本题考查了轴对称最短距离问题,两点间的距离公式,图象与坐标的关系,把求代数式的最小值转化为最短距离问题是解题的关键.

练习册系列答案
相关题目
5.学校建围栏,要为24000根栏杆油漆,由于改进了技术,每天比原计划多油400根,结果提前两天完成了任务,请问原计划每天油多少根栏杆?如果设原计划每天油x根栏杆,根据题意列方程为( )
| A. | $\frac{24000}{x}$=$\frac{24000}{x-400}$+2 | B. | $\frac{24000}{x}$=$\frac{24000}{x-400}$-2 | ||
| C. | $\frac{24000}{x}$=$\frac{24000}{x+400}$-2 | D. | $\frac{24000}{x}$=$\frac{24000}{x+400}$+2 |
9.将多项式a2+6a-16因式分解正确的是( )
| A. | (a-2)(a-8) | B. | (a+2)(a-8) | C. | (a-2)(a+8) | D. | (a+2)(a+8) |
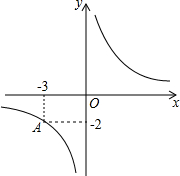 如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(-3,-2).
如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(-3,-2).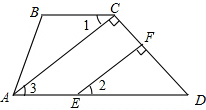 如图,在四边形ABCD中,∠BAD=103°-∠2,∠B=77°+∠2,AC⊥CD于F,∠1和∠2相等吗?请把结论或理由填写在下列红线或括号中.
如图,在四边形ABCD中,∠BAD=103°-∠2,∠B=77°+∠2,AC⊥CD于F,∠1和∠2相等吗?请把结论或理由填写在下列红线或括号中.