题目内容
6.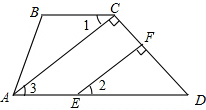 如图,在四边形ABCD中,∠BAD=103°-∠2,∠B=77°+∠2,AC⊥CD于F,∠1和∠2相等吗?请把结论或理由填写在下列红线或括号中.
如图,在四边形ABCD中,∠BAD=103°-∠2,∠B=77°+∠2,AC⊥CD于F,∠1和∠2相等吗?请把结论或理由填写在下列红线或括号中.说明:∵∠BAD=103°-∠2,∠B=77°+∠2(已知)
∴∠BAD+∠B=180°(等式性质)
∴AD∥BC(同旁内角互补,两直线平行)
∴∠1=∠3(两直线平行,内错角相等)
∵AC⊥CD,EF⊥CD(已知)
∴∠ACD=∠EFD=90°(垂直的定义)
∴AC∥EF(同位角相等,两直线平行)
∴∠2=∠3(两直线平行,同位角相等)
∴∠1=∠2(等量代换)
分析 根据同旁内角互补,两直线平行先求出AD∥BC,然后根据两直线平行,内错角相等求出∠1=∠DBC,再根据垂直于同一直线的两直线互相平行求出BD∥EF,然后根据两直线平行,同位角相等即可得解.
解答 解:∵∠BAD=103°-∠2,∠B=77°+∠2(已知)
∴∠BAD+∠B=180°(等式性质)
∴AD∥BC (同旁内角互补,两直线平行 )
∴∠1=∠3( 两直线平行,内错角相等)
∵AC⊥CD,EF⊥CD(已知)
∴∠ACD=∠EFD=90°(垂直的定义)
∴AC∥EF(同位角相等,两直线平行)
∴∠2=∠3( 两直线平行,同位角相等)
∴∠1=∠2(等量代换)
故答案为:AD∥BC;同旁内角互补,两直线平行; 两直线平行,内错角相等;垂直的定义;同位角相等,两直线平行;∠2=∠3; 两直线平行,同位角相等;等量代换.
点评 本题考查了平行线的判定与性质,准确识图,并熟练掌握平行线的性质与判定方法是解题的关键.

练习册系列答案
相关题目
1.在实数$\frac{π}{2}$、$\sqrt{12}$、$\sqrt{16}$、$\root{3}{-27}$、$\frac{22}{7}$、3.14、0.3030030003中,无理数有2个.
11.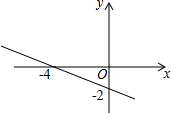 一次函数y=kx+b的图象如图所示,则不等式kx+b<0的解集是( )
一次函数y=kx+b的图象如图所示,则不等式kx+b<0的解集是( )
 一次函数y=kx+b的图象如图所示,则不等式kx+b<0的解集是( )
一次函数y=kx+b的图象如图所示,则不等式kx+b<0的解集是( )| A. | x>-2 | B. | x<-2 | C. | x>-4 | D. | x<-4 |
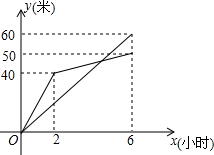 甲乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(米)与挖掘时间x(小时)之间的关系如图所示,甲乙两队在施工过程中所挖河渠的长度相等的时间为4小时.
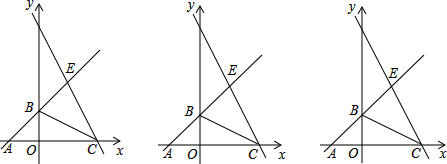
甲乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(米)与挖掘时间x(小时)之间的关系如图所示,甲乙两队在施工过程中所挖河渠的长度相等的时间为4小时.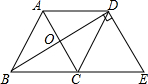 如图,在菱形ABCD中,点O是对角线AC、BD的交点,点E是BC边延长线上一点,且BD⊥DE.
如图,在菱形ABCD中,点O是对角线AC、BD的交点,点E是BC边延长线上一点,且BD⊥DE.