题目内容
17．先化简，再求值：$\frac{m-4}{{m}^{2}-9}$•（1-$\frac{14m-7}{{m}^{2}-8m+16}$）÷$\frac{1}{m-3}$．其中m=5．分析 原式括号中两项通分并利用同分母分式的减法法则计算，再利用除法法则变形，约分得到最简结果，把m的值代入计算即可求出值．
解答 解：原式=$\frac{m-4}{（m+3）（m-3）}$•$\frac{{m}^{2}-8m+16-14m+7}{（m-4）^{2}}$•（m-3）
=$\frac{{m}^{2}-22m+23}{（m+3）（m-4）}$，
当m=5时，原式=$\frac{25-110+23}{8}$=-$\frac{31}{4}$．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
12．当b＜0时，一次函数y=2x+b的图象经过（ ）
| A． | 第一、二、三象限 | B． | 第一、二、四象限 | C． | 第二、三、四象限 | D． | 第一、三、四象限 |
2．
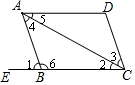如图，四边形ABCD，E是CB延长线上一点，下列推理正确的是（ ）
如图，四边形ABCD，E是CB延长线上一点，下列推理正确的是（ ）| A． | 如果∠1=∠2，那么AB∥CD | B． | 如果∠3=∠4，那么AD∥BC | ||
| C． | 如果AD∥BC，那么∠6+∠BAD=180° | D． | 如果∠6+∠BCD=180°，那么AD∥BC |
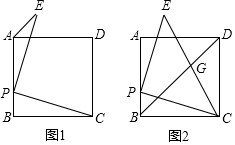
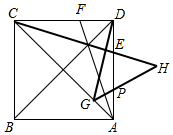在正方形ABCD中，DE=DF，DG⊥CE，交CA于G，GH⊥AF，交AD于P，交CE延长线于H，请问三条粗线DG，GH，CH的数量关系．