题目内容
7.已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)的对应值如下表所示:| … | 0 | 50 | 200 | … | |
| y | … | 1 | -1 | 1 | … |
| A. | x1=x2=100 | B. | x1=0,x2=200 | C. | x1=50,x2=150 | D. | x1=50,x2=250 |
分析 设抛物线解析式为y=ax2+bx+c,把(0,1),(50,-1),(200,1)分别代入求出a,b的值,即可求出方程ax2+bx+2=0的根.
解答 解:
设抛物线解析式为y=ax2+bx+c,把(0,1),(50,-1),(200,1)分别代入得:
$\left\{\begin{array}{l}{1=c}\\{-1=2500a+50b+c}\\{1=40000a+200b+c}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{3750}}\\{b=-\frac{4}{75}}\\{c=1}\end{array}\right.$,
∴ax2+bx+2=0的根即为方程x2-200x+7500=0的根,
解得:x1=50,x2=150,
故选C.
点评 本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
17.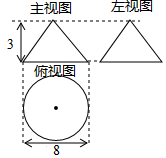 已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积是( )
已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积是( )
 已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积是( )
已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积是( )| A. | 40π | B. | 24π | C. | 20 π | D. | 12π |
18.两名同学都进行了5次立定跳远测试.经计算,他们的平均成绩相同,若要比较这两名同学的成绩谁更稳定,通常还需要比较他们成绩的( )
| A. | 众数 | B. | 中位数 | C. | 方差 | D. | 以上都不对 |
15. 如图,从一块直径为4$\sqrt{2}$cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
如图,从一块直径为4$\sqrt{2}$cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
 如图,从一块直径为4$\sqrt{2}$cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
如图,从一块直径为4$\sqrt{2}$cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )| A. | 2$\sqrt{2}$cm | B. | $\sqrt{2}$cm | C. | 1 cm | D. | 2cm |
12.下列计算正确的是( )
| A. | a+a=a2 | B. | a•a2=a3 | C. | (-a3)2=a9 | D. | (3a)3=9a3 |
16.事件A:掷一次骰子,向上一面的点数是5;事件B:买一张彩票,有一注号码中奖了,则( )
| A. | 事件A和B都是随机事件 | |
| B. | 事件A是随机事件,事件B是不可能事件 | |
| C. | 事件A是必然事件,事件B是随机事件 | |
| D. | 事件A和事件B都是必然事件 |
20.将方程2x+y=1转化为用含x的代数式表示的形式,正确的是( )
| A. | y=-2x+1 | B. | y=1+2x | C. | -y=2x+1 | D. | y-1=2x |
 如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.
如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.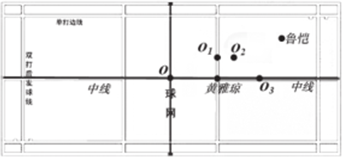 2017 全英羽毛球公开赛混双决赛,中国组合鲁恺/黄雅琼,对阵马来西亚里约奥运亚军陈炳顺/吴柳萤,鲁恺/黄雅琼两名小将的完美配合结果获胜.如图是羽毛球场地示意图,x 轴平行场地的中线,y 轴平行场地的球网线,设定鲁恺的坐标是(3,1),黄雅琼的坐标是(0,-1),则坐标原点为( )
2017 全英羽毛球公开赛混双决赛,中国组合鲁恺/黄雅琼,对阵马来西亚里约奥运亚军陈炳顺/吴柳萤,鲁恺/黄雅琼两名小将的完美配合结果获胜.如图是羽毛球场地示意图,x 轴平行场地的中线,y 轴平行场地的球网线,设定鲁恺的坐标是(3,1),黄雅琼的坐标是(0,-1),则坐标原点为( )