题目内容
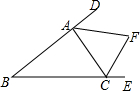如图，已知∠CAD和∠ACE的平分线AF、CF相交于点F．求证：点F在∠DBE的角平分线上．考点：角平分线的性质
专题：证明题
分析：过F作FM⊥BA于M，FN⊥BC于N，FQ⊥AC于Q，根据角平分线性质得出FM=FQ=FN，再根据角平分线性质得出即可．
解答：
证明：过F作FM⊥BA于M，FN⊥BC于N，FQ⊥AC于Q，
∵∠CAD和∠ACE的平分线AF、CF相交于点F，
∴FM=FQ，FQ=FN，
∴FM=FN，
∵FM⊥BA，FN⊥BC，
∴点F在∠DBE的角平分线上．
证明：过F作FM⊥BA于M，FN⊥BC于N，FQ⊥AC于Q，
∵∠CAD和∠ACE的平分线AF、CF相交于点F，
∴FM=FQ，FQ=FN，
∴FM=FN，
∵FM⊥BA，FN⊥BC，
∴点F在∠DBE的角平分线上．
点评：本题考查了角平分线性质的应用，注意：角平分线上的点到角两边的距离相等．
练习册系列答案
相关题目
如图，在△ABC中，分别以AB、AC为边作等边△ABE，等边△ACD，BD与CE相交于点O，连接AO，求证：AO平分∠DOE．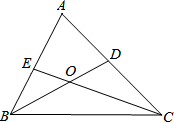
如图，已知：△ABC中，BD、CE分别是△ABC的两条角平分线，相交于点O．