题目内容
20.(1)计算:|$\sqrt{3}$-3|+(π-1)0-(-$\frac{1}{2}$)-2+$\root{3}{8}$(2)$\frac{1}{2}$(x-2)2=8,求x.
分析 (1)本题涉及绝对值、零指数幂、负整数指数幂、三次根式化简四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;
(2)先系数化为1,再开平方即可求得x的值.
解答 解:(1)|$\sqrt{3}$-3|+(π-1)0-(-$\frac{1}{2}$)-2+$\root{3}{8}$
=3-$\sqrt{3}$+1-4+2
=2-$\sqrt{3}$
(2)$\frac{1}{2}$(x-2)2=8,
(x-2)2=16,
x-2=±4,
解得x1=-2,x2=6.
点评 本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握绝对值、零指数幂、负整数指数幂、三次根式化简等考点的运算.同时考查了开平方的方法解方程.

练习册系列答案
相关题目
10.下面的计算正确的是( )
| A. | a+2a=3a2 | B. | a3÷a=3 | C. | a2•a3=a5 | D. | -(a)3=a3 |
12.a=5+2$\sqrt{6}$,b=$\frac{{\sqrt{3}+\sqrt{2}}}{{\sqrt{3}-\sqrt{2}}}$,则a与b的关系是( )
| A. | a=b | B. | ab=1 | C. | a>b | D. | a<b. |
10.式子$\frac{1}{x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x>2 | B. | x≥2 | C. | x≠2 | D. | x≠-2 |
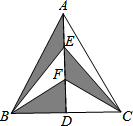 如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的三等分点,若△ABC的面积为12cm2,则图中的阴影面积是6cm2.
如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的三等分点,若△ABC的面积为12cm2,则图中的阴影面积是6cm2.