题目内容
1.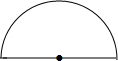 如图,某仓库入口的截面是一个半径为12米的半圆形,一个长、宽、高分别是12米,10米,8米的集装箱能放进这个仓库吗?请通过计算说明.
如图,某仓库入口的截面是一个半径为12米的半圆形,一个长、宽、高分别是12米,10米,8米的集装箱能放进这个仓库吗?请通过计算说明.
分析 设ABCD是矩形,作OE⊥AB与E,首先根据垂径定理求得AE=5米,然后根据勾股定理求得OE的长,再与箱子的高比较即可判定.
解答  解:如图,设ABCD是矩形,则AB∥CD,AB=CD=10米,OA=12米,
解:如图,设ABCD是矩形,则AB∥CD,AB=CD=10米,OA=12米,
作OE⊥AB与E,则OE平分AB,
∴AE=$\frac{1}{2}$AB=5米,
∴OE2=OA2-AE2=122-52=119,
∵82=64,119>64,
∴长、宽、高分别是12米,10米,8米的集装箱能放进这个仓库.
点评 本题考查了勾股定理的应用以及垂径定理,将实际问题转化为数学问题是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.用代数式表示“x的2倍与y的平方的和”,正确的是( )
| A. | 2x2+y2 | B. | 2x+y2 | C. | 2(x+y2) | D. | 2(x+y)2 |
6.我们将宽与长的比是黄金比的矩形称为黄金矩形.已知矩形ABCD是黄金矩形且长AB=10,则宽BC为( )
| A. | 2$\sqrt{5}$-2 | B. | 5$\sqrt{5}$-5 | C. | 15-5$\sqrt{5}$ | D. | 0.618 |
13.用一条长40cm的绳子怎样围成一个面积为75cm2的矩形?设矩形的一边为x米,根据题意,可列方程为( )
| A. | x(40-x)=75 | B. | x(20-x)=75 | C. | x(x+40)=75 | D. | x(x+20)=75 |
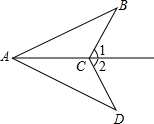 如图,已知△ABC≌△ADC,∠1=64°,则∠2的度数是64°.
如图,已知△ABC≌△ADC,∠1=64°,则∠2的度数是64°.
 如图,AB⊥BC,DC⊥BC,AE⊥CD,∠DAE=30°,∠DBC=45°,AB=2,求CD.
如图,AB⊥BC,DC⊥BC,AE⊥CD,∠DAE=30°,∠DBC=45°,AB=2,求CD.