题目内容
4.求2x2+6x-3的最小值.分析 利用配方法把原式化为含有完全平方的形式,根据偶次方的非负性解答即可.
解答 解:2x2+6x-3
=2(x2+3x+$\frac{9}{4}$)-$\frac{9}{2}$-3
=2(x+$\frac{3}{2}$)2-$\frac{15}{2}$,
∵(x+$\frac{3}{2}$)2≥0,
∴2(x+$\frac{3}{2}$)2-$\frac{15}{2}$的最小值是-$\frac{15}{2}$,即2x2+6x-3的最小值是-$\frac{15}{2}$.
点评 本题考查的是配方法的应用,掌握完全平方公式、偶次方的非负性是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
9.声音在空气中的传播速度约为340m/s,这个数字用科学记数法表示为( )
| A. | 34×10 | B. | 3.4×103 | C. | 3.4×102 | D. | 0.34×103 |
8.矩形ABCD中,AB=8,BC=3$\sqrt{5}$,点P在边AB上,且AP=2,如果圆P是以点P为圆心,PD为半径的圆,那么下列判断正确的是( )
| A. | 点B、C均在圆P外 | B. | 点B在圆P外、点C在圆P内 | ||
| C. | 点B在圆P内、点C在圆P外 | D. | 点B、C均在圆P内 |
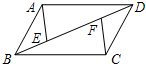 如图,在?ABCD中,E,F是对角线BD上的两点且BE=DF,联结AE,CF.
如图,在?ABCD中,E,F是对角线BD上的两点且BE=DF,联结AE,CF. 如图,BD是?ABCD的对角线,BE=EF=$\frac{1}{2}$FD,则S△AMH:S?ABCD=$\frac{1}{3}$.
如图,BD是?ABCD的对角线,BE=EF=$\frac{1}{2}$FD,则S△AMH:S?ABCD=$\frac{1}{3}$.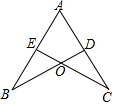 如图,已知∠B=∠C,要判断△ABD≌△ACE,若根据“ASA”,还需要的条件是AB=AC若根据“AAS”,则还需要的条件是BD=CE或AD=AE.
如图,已知∠B=∠C,要判断△ABD≌△ACE,若根据“ASA”,还需要的条件是AB=AC若根据“AAS”,则还需要的条件是BD=CE或AD=AE. 如图,已知在平行四边形ABCD中,对角线AC,BD相交于点O,EF经过点O,且分别与AD,BC交于E,F.证明:AE=CF.
如图,已知在平行四边形ABCD中,对角线AC,BD相交于点O,EF经过点O,且分别与AD,BC交于E,F.证明:AE=CF.