题目内容
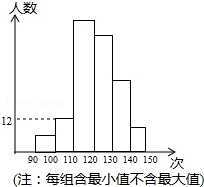 某民族学校对七年级学生进行跳绳测试,并抽取了部分学生的一分钟跳绳测试成绩进行整理,作出如图统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出第一组的频率为0.04,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:
某民族学校对七年级学生进行跳绳测试,并抽取了部分学生的一分钟跳绳测试成绩进行整理,作出如图统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出第一组的频率为0.04,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:(1)这次共抽取了多少名学生的一分钟跳绳测试成绩?
(2)若跳绳次数不少于130次为优秀,则随意抽取一名学生的测试成绩为优秀的概率是多少?
(3)如果这次测试成绩中的中位数是120次,那么这次测试中,成绩为120次的学生至少有多少人?
考点:频数(率)分布直方图,中位数,概率公式
专题:
分析:1)根据题意:结合各小组频数之和等于数据总和,各小组频率之和等于1;易得第二组的频率0.08;再由频率、频数的关系频率=
,可得总人数.
(2)根据题意:从左至右第二、三、四组的频数比为4:17:15,求得第三组和第四组的频数,求得后边两组的频率的和就是优秀率;
(3)由中位数的意义,作答即可.
| 频数 |
| 总数 |
(2)根据题意:从左至右第二、三、四组的频数比为4:17:15,求得第三组和第四组的频数,求得后边两组的频率的和就是优秀率;
(3)由中位数的意义,作答即可.
解答:
解:(1)抽取的总人数是:12÷(0.12-0.04)=150(人);
(2)第二组的频率是:0.12-0.04=0.08,
则第三组的频率是:0.08×
=0.34,第四组的频率是:0.08×
=0.30,
则测试成绩为优秀的概率是:1-0.12-0.34-0.30=0.24;
(3)前三组的人数为150×(0.12+0.34)=69,
而中位数是第75和第76个数的平均数,而120是第四组中最小的数值,因而第75和第76都是120,所以成绩为120次的学生至少有76-69=7人.
(2)第二组的频率是:0.12-0.04=0.08,
则第三组的频率是:0.08×
| 17 |
| 4 |
| 15 |
| 4 |
则测试成绩为优秀的概率是:1-0.12-0.34-0.30=0.24;
(3)前三组的人数为150×(0.12+0.34)=69,
而中位数是第75和第76个数的平均数,而120是第四组中最小的数值,因而第75和第76都是120,所以成绩为120次的学生至少有76-69=7人.
点评:本题考查了中位数的运用和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.同时对频率、频数灵活运用的综合考查,各小组频数之和等于数据总和,各小组频率之和等于1.频率、频数的关系频率=
.
| 频数 |
| 总数 |

练习册系列答案
相关题目
“神州”五号飞船总重7990000克,用科学记数法表示为( )
| A、0.799×107克 |
| B、8×106克 |
| C、8.0×106克 |
| D、7.99×106克 |
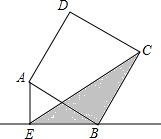 如图,正方形ABCD的边长是5,点B在直线BE上,AE⊥BE于E,AE=3.则△BCE的面积为
如图,正方形ABCD的边长是5,点B在直线BE上,AE⊥BE于E,AE=3.则△BCE的面积为 如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA,A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=-x2+2x+
如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA,A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=-x2+2x+ 如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,且AC=FC.求证:AC是⊙O的切线.
如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,且AC=FC.求证:AC是⊙O的切线.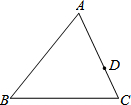 如图,在△ABC中,∠C>∠B,AB=12,AC=9,D是AC上一点,AD=6,在AB上取一点E,使以A,D,E三点为顶点的三角形与△ABC相似,则AE的长为
如图,在△ABC中,∠C>∠B,AB=12,AC=9,D是AC上一点,AD=6,在AB上取一点E,使以A,D,E三点为顶点的三角形与△ABC相似,则AE的长为