题目内容
5.已知△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,若$\widehat{EF}$=$\widehat{DE}$,如图1.(1)判断△ABC的形状,并证明你的结论;
(2)设AE与DF相交于点M,如图2,AF=2FC=4,求AM的长.
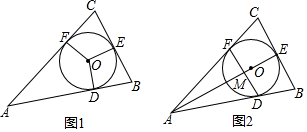
分析 (1)易证∠EOF+∠C=180°,∠DOE+∠B=180°和∠EOF=∠DOE,即可解题;
(2)连接OB、OC、OD、OF,易证AD=AF,BD=CF可得DF∥BC,再根据AE长度即可解题.
解答 解:(1)△ABC为等腰三角形,
∵△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,
∴∠CFE=∠CEF=∠BDO=∠BEO=90°,
∵四边形内角和为360°,
∴∠EOF+∠C=180°,∠DOE+∠B=180°,
∵$\widehat{EF}$=$\widehat{DE}$,
∴∠EOF=∠DOE,
∴∠B=∠C,AB=AC,
∴△ABC为等腰三角形;
(2)连接OB、OC、OD、OF,如图,
∵等腰三角形ABC中,AE⊥BC,
∴E是BC中点,BE=CE,
∵在Rt△AOF和Rt△AOD中,$\left\{\begin{array}{l}{OD=OF}\\{OA=OA}\end{array}\right.$,
∴Rt△AOF≌Rt△AOD,
∴AF=AD,
同理Rt△COF≌Rt△COE,CF=CE=2,
Rt△BOD≌Rt△BOE,BD=BE,
∴AD=AF,BD=CF,
∴DF∥BC,
∴$\frac{AM}{AE}$=$\frac{AF}{AC}$,
∵AE=$\sqrt{{AC}^{2}{-CE}^{2}}$=4$\sqrt{2}$,
∴AM=4$\sqrt{2}$×$\frac{2}{3}$=$\frac{8\sqrt{2}}{3}$.
点评 本题考查了全等三角形的判定和性质,考查了等腰三角形的性质,考查了圆的切线的性质,本题中求DF∥BC是解题的关键.

练习册系列答案
相关题目
16. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PH•PC
其中正确的是( )
 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PH•PC
其中正确的是( )
| A. | ①②③④ | B. | ②③ | C. | ①②④ | D. | ①③④ |
13.已知A,B两点分别在反比例函数y=$\frac{3m}{x}$(m≠0)和y=$\frac{2m-5}{x}$(m≠$\frac{5}{2}$)的图象上,若点A与点B关于x轴对称,则m的值为1.
20.观察以下一列数的特点:0,1,-4,9,-16,25,…,则第11个数是( )
| A. | -121 | B. | -100 | C. | 100 | D. | 121 |
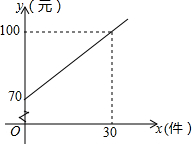 某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.
某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.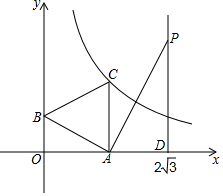 如图,一次函数y=-$\frac{{\sqrt{3}}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
如图,一次函数y=-$\frac{{\sqrt{3}}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC. 如图,平面直角坐标系中,已知直线y=x上一点P(2,2)C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q.
如图,平面直角坐标系中,已知直线y=x上一点P(2,2)C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q.