题目内容
 如图,AF⊥BC,CE⊥AB,则图中相似的三角形有
如图,AF⊥BC,CE⊥AB,则图中相似的三角形有考点:相似三角形的判定
专题:
分析:根据相似三角形的判定,可判定共5对三角形相似.
解答: 解:如图,①∵AF⊥BC,CE⊥AB,
解:如图,①∵AF⊥BC,CE⊥AB,
∴∠AED=∠CFD=90°.
又∵∠ADE=∠CDF,
∴△AED∽△CFD.
②∵AF⊥BC,CE⊥AB,
∴∠AFB=∠CEB=90°.
又∵∠B=∠B,
∴△AFB∽△CEB;
③∵∠A=∠A,∠AED=∠AFB=90°,
∴△AED∽△AFB;
④∵∠C=∠C,∠CFD=∠CEB,
∴△CFD∽△CEB,
⑤△AED∽△CEB;
故答案是:5.
 解:如图,①∵AF⊥BC,CE⊥AB,
解:如图,①∵AF⊥BC,CE⊥AB,∴∠AED=∠CFD=90°.
又∵∠ADE=∠CDF,
∴△AED∽△CFD.
②∵AF⊥BC,CE⊥AB,
∴∠AFB=∠CEB=90°.
又∵∠B=∠B,
∴△AFB∽△CEB;
③∵∠A=∠A,∠AED=∠AFB=90°,
∴△AED∽△AFB;
④∵∠C=∠C,∠CFD=∠CEB,
∴△CFD∽△CEB,
⑤△AED∽△CEB;
故答案是:5.
点评:本题考查相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角.

练习册系列答案
相关题目
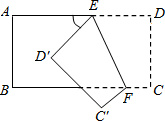 如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置.若∠AED′=50°,则∠DEF等于( )
如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置.若∠AED′=50°,则∠DEF等于( )| A、50° | B、65° |
| C、75° | D、60° |

 △ABC中∠A:∠B:∠C=3:5:10,又△A′B′C≌△ABC,且B′、C、A在同一直线上,则∠BC A′:∠BC B′=
△ABC中∠A:∠B:∠C=3:5:10,又△A′B′C≌△ABC,且B′、C、A在同一直线上,则∠BC A′:∠BC B′=