题目内容
10.先化简,再求值:(1)(a+b)(a-b)-(a+b)2+2b2,其中$a=\frac{1}{2}$,b=2
(2)$\frac{2m+2n}{{{m^2}-{n^2}}}$,其中m=-1,n=-2.
分析 (1)原式利用平方差公式及完全平方公式化简,去括号合并得到最简结果,把a与b的值代入计算即可求出值;
(2)原式约分得到最简结果,把m与n的值代入计算即可求出值.
解答 解:(1)原式=a2-b2-a2-2ab-b2+2b2=-2ab,
当a=$\frac{1}{2}$,b=2时,原式=-2;
(2)原式=$\frac{2(m+n)}{(m+n)(m-n)}$=$\frac{2}{m-n}$,
当m=-1,n=-2时,原式=2.
点评 此题考查了分式的化简求值,以及整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.-24的值是( )
| A. | -8 | B. | 8 | C. | 16 | D. | -16 |
19.把方程$\frac{1}{2}x=1$变形为x=2,其依据是( )
| A. | 等式的两边同时乘以$\frac{1}{2}$ | B. | 等式的两边同时除以$\frac{1}{2}$ | ||
| C. | 等式的两边同时减去$\frac{1}{2}$ | D. | 等式的两边同时加上$\frac{1}{2}$ |
20.一个角的余角是30度,则这个角的补角是( )
| A. | 45度 | B. | 60度 | C. | 90度 | D. | 120度 |
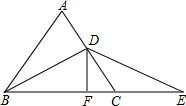 已知,如图,△ABC是等边三角形,BD是AC边上的高,延长BC到E,使CE=CD,过D作DF⊥BE于F.
已知,如图,△ABC是等边三角形,BD是AC边上的高,延长BC到E,使CE=CD,过D作DF⊥BE于F.