题目内容
11.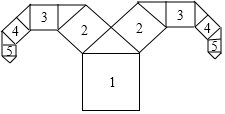 如图所示是一种“牛头形”图案,其作法是:从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,依此类推下去,若正方形1的边长为16cm,则正方形6的边长为( )
如图所示是一种“牛头形”图案,其作法是:从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,依此类推下去,若正方形1的边长为16cm,则正方形6的边长为( )| A. | 1cm | B. | 2$\sqrt{2}$cm | C. | 3cm | D. | 4cm |
分析 根据等腰直角三角形直角边等于斜边的$\frac{\sqrt{2}}{2}$倍,求出第n个正方形的边长与第1个正方形的边长的关系式,然后把正方形1的边长16cm代入进行计算即可得解.
解答 解:根据题意,设正方形1的边长为a,则正方形2的边长为$\frac{\sqrt{2}}{2}$a,
正方形3的边长为:($\frac{\sqrt{2}}{2}$)2a,
正方形4的边长为:($\frac{\sqrt{2}}{2}$)3a,
…,
依此类推,正方形n的边长为:($\frac{\sqrt{2}}{2}$)n-1a,
∵正方形1的边长为16cm,
∴正方形6的边长为:($\frac{\sqrt{2}}{2}$)6-1×16=2$\sqrt{2}$cm.
故选B.
点评 本题考查了正方形的性质,等腰直角三角形的性质直角边等于斜边的$\frac{\sqrt{2}}{2}$倍的性质,求出第n个正方形的边长与第1个正方形的边长的关系式是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 如图,点A是圆弧BC上一点,用尺规作图法找出圆心O点(保留作图痕迹,不写做法)
如图,点A是圆弧BC上一点,用尺规作图法找出圆心O点(保留作图痕迹,不写做法)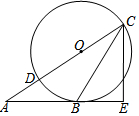 如图,已知△ABC的边AB是⊙O的切线,切点为B,AC经过圆心O并与圆相交于点D、C.过C作直线CE⊥AB,交AB的延长线于点E.
如图,已知△ABC的边AB是⊙O的切线,切点为B,AC经过圆心O并与圆相交于点D、C.过C作直线CE⊥AB,交AB的延长线于点E.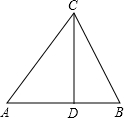 已知:如图,在△ABC中,CD⊥AB,sinA=$\frac{4}{5}$,AB=13,CD=12.
已知:如图,在△ABC中,CD⊥AB,sinA=$\frac{4}{5}$,AB=13,CD=12.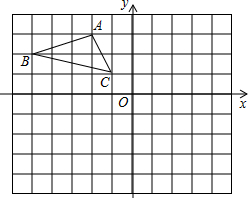 如图,△ABC在第二象限内,顶点A的坐标是(-2,3),
如图,△ABC在第二象限内,顶点A的坐标是(-2,3),