题目内容
16.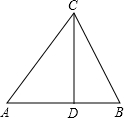 已知:如图,在△ABC中,CD⊥AB,sinA=$\frac{4}{5}$,AB=13,CD=12.
已知:如图,在△ABC中,CD⊥AB,sinA=$\frac{4}{5}$,AB=13,CD=12.求:AC的长和tanB的值.
分析 首先根据正弦的定义及CD的长求得AC的长,然后利用勾股定理求得AD的长,从而根据AB的长求得BD的长,利用正切的定义求得∠B的正切即可.
解答 解:∵CD⊥AB,sinA=$\frac{CD}{AC}$=$\frac{4}{5}$,CD=12,
∴AC=CD×$\frac{5}{4}$=15,
∴AD=9,
∵AB=13,
∴BD=AB-AD=13-9=4,
∴tanB=$\frac{CD}{BD}$=$\frac{12}{4}$=3.
点评 本题考查了解直角三角形的知识,解题的关键是能够选择合适的边角关系,难度不大.

练习册系列答案
相关题目
11.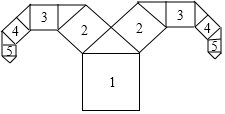 如图所示是一种“牛头形”图案,其作法是:从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,依此类推下去,若正方形1的边长为16cm,则正方形6的边长为( )
如图所示是一种“牛头形”图案,其作法是:从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,依此类推下去,若正方形1的边长为16cm,则正方形6的边长为( )
 如图所示是一种“牛头形”图案,其作法是:从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,依此类推下去,若正方形1的边长为16cm,则正方形6的边长为( )
如图所示是一种“牛头形”图案,其作法是:从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,依此类推下去,若正方形1的边长为16cm,则正方形6的边长为( )| A. | 1cm | B. | 2$\sqrt{2}$cm | C. | 3cm | D. | 4cm |
1.在下列方程中,一元二次方程是( )
| A. | x2-2xy+y2=0 | B. | x2-2x=3 | C. | x(x+3)=x2-1 | D. | x+$\frac{1}{x}$=0 |
8.将y=x2向右平移1个单位,再向下平移2单位后,所得表达式是( )
| A. | y=(x-1)2+2 | B. | y=(x+1)2+2 | C. | y=(x-1)2-2 | D. | y=(x+1)2-2 |
 如图,在△ABC中,AB=6,BC=8,AC=4,D、E、F分别为BC、AC、AB中点,连接DE、FE,则四边形BDEF的周长是14.
如图,在△ABC中,AB=6,BC=8,AC=4,D、E、F分别为BC、AC、AB中点,连接DE、FE,则四边形BDEF的周长是14.