题目内容
12.为解决沙区拥堵问题,在三峡广场附近拟建一个地下长方形车库ABCD,图案设计如图所示,已知长方形ABCD长为300米,宽为200米,在长方形ABCD内部修等宽为x米的安全通道,四角修完全一样的正方形临时停车位,且正方形临时停车位的边长为(x+50)米,若安全通道铺红色地胶,临时停车位铺黄色地胶,其余部分铺绿色地胶.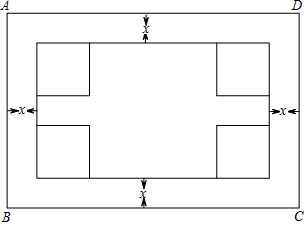
(1)请用含x的代数式表示铺绿色地胶部分的面积,并将所得式子化简;
(2)如果铺红色地胶的费用为每平方米60元,铺黄色地胶的费用为每平方米50元,铺绿色地胶的费用为每平方米40元,设铺地下车库地面的总费用为y元,请用含x的代数式表示y,并将所得式子化简;
(3)在(2)的条件下,求当x=2时,求铺地下车库地面的总费用.
分析 (1)铺绿色地胶部分的面积=里面小长方形的面积-4个正方形临时停车位的面积,依此即可求解;
(2)分别求出铺红色地胶的面积,铺黄色地胶的面积,铺绿色地胶的面积,再乘以它们的单价,相加即可求解;
(3)把x=2代入计算即可求解.
解答 解:(1)(300-2x)×(200-2x)-4(x+50)2
=60000-600x-400x+4x2-4x2-400x-10000
=50000-1400x;
(2)60(300×2x+200×2x-4x2)+50×4(x+50)2+40(50000-1400x)
=60(1000x-4x2)+200(x2+100x+2500)+2000000-56000x
=60000x-240x2+200x2+20000x+500000+2000000-56000x
=-40x2+24400x+2500000;
(3)当x=2时,
-40x2+24400x+2500000
=-160+48800+2500000
=2548640.
点评 本题考查了整式的混合运算,解答本题的关键是表示出铺红色地胶的面积,铺黄色地胶的面积,铺绿色地胶的面积,难度一般.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
1.$\frac{1}{5}$的相反数为( )
| A. | 5 | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | -5 |
3.观察表格
写出一个y关于x的函数解析式y=1.8x+32.
| x | … | 10 | 20 | 30 | 40 | 50 | … |
| y | … | 50 | 68 | 86 | 104 | 122 | … |
7. 某蔬菜基地要把一批新鲜蔬菜运往外地,有汽车和火车两种运输方式可供选择,其中汽车运输的主要参考数据如下表:
某蔬菜基地要把一批新鲜蔬菜运往外地,有汽车和火车两种运输方式可供选择,其中汽车运输的主要参考数据如下表:
火车运输总费用y2(元)与运输路程x(km)之间的函数图象如图所示:
(1)请分别写出汽车、火车运输的总费用y1(元)、y2(元)与运输路程x(km)之间的函数关系;
(2)若蔬菜基地先由汽车把蔬菜运往60km外的中转站再用火车运送(中转时间忽略不计),写出运输总费用y与运输总路程x(km)之间的函数关系,并求出当运输总路程为200km时的总费用;
(3)若只选择一种运输方式,你认为哪种运输方式运输的总费用较少?并说明理由.
 某蔬菜基地要把一批新鲜蔬菜运往外地,有汽车和火车两种运输方式可供选择,其中汽车运输的主要参考数据如下表:
某蔬菜基地要把一批新鲜蔬菜运往外地,有汽车和火车两种运输方式可供选择,其中汽车运输的主要参考数据如下表:| 运输方式 | 汽车 |
| 运输速度(km/h) | 60 |
| 装卸费用(元) | 200 |
| 途中综合费用(元/小时) | 300 |
(1)请分别写出汽车、火车运输的总费用y1(元)、y2(元)与运输路程x(km)之间的函数关系;
(2)若蔬菜基地先由汽车把蔬菜运往60km外的中转站再用火车运送(中转时间忽略不计),写出运输总费用y与运输总路程x(km)之间的函数关系,并求出当运输总路程为200km时的总费用;
(3)若只选择一种运输方式,你认为哪种运输方式运输的总费用较少?并说明理由.