题目内容
7.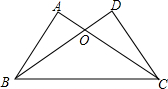 如图,已知:∠A=∠D=90°,AC=DB,求证:OB=OC.
如图,已知:∠A=∠D=90°,AC=DB,求证:OB=OC.以下是小明同学的分析思路:
先利用已知条件,可以证明Rt△ABC≌Rt△ABC,依据是“HL”,进而得到AB=DC;
再证明△ABO≌△DCO,依据是“AAS”此时,就能够证出
OB=OC.
分析 因为∠A=∠D=90°,AC=BD,BC=BC,知Rt△BAC≌Rt△CDB(HL),所以AB=CD,证明△ABO与△CDO全等,所以有OB=OC.
解答 解:可以证明Rt△ABC≌Rt△ABC,依据是“HL”,进而得到AB=DC;
再证明△ABO≌△DCO,依据是“AAS”此时,就能够证出
OB=OC,
故答案为:HL;△ABO;△DCO;AAS.
点评 本题考查了直角三角形的判定和性质;由三角形全等得角相等,从而得到线段相等是证明题中常用的方法,注意掌握应用.

练习册系列答案
相关题目
2. 如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BA=4m,CA=0.8m,则树的高度为( )
如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BA=4m,CA=0.8m,则树的高度为( )
 如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BA=4m,CA=0.8m,则树的高度为( )
如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BA=4m,CA=0.8m,则树的高度为( )| A. | 4.8m | B. | 6.4m | C. | 8m | D. | 10m |
12. 如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于4,则△ABC的面积等于( )
如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于4,则△ABC的面积等于( )
 如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于4,则△ABC的面积等于( )
如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于4,则△ABC的面积等于( )| A. | 12 | B. | 16 | C. | 24 | D. | 36 |
17. 如图,直径为1个单位长度的圆从原点沿数轴向右无滑动地滚动一周,原点滚到了点A,下列说法正确的( )
如图,直径为1个单位长度的圆从原点沿数轴向右无滑动地滚动一周,原点滚到了点A,下列说法正确的( )
 如图,直径为1个单位长度的圆从原点沿数轴向右无滑动地滚动一周,原点滚到了点A,下列说法正确的( )
如图,直径为1个单位长度的圆从原点沿数轴向右无滑动地滚动一周,原点滚到了点A,下列说法正确的( )| A. | 点A所表示的是π | B. | OA上只有一个无理数π | ||
| C. | 数轴上无理数和有理数一样多 | D. | 数轴上的有理数比无理数要多一些 |
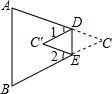 如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=30°,求∠2的度数.
如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=30°,求∠2的度数. 如图所示的运算程序中,若开始输入的x值为36,我们发现第1次输出的结果为18,第2次输出的结果为9,第2016次输出的结果为6.
如图所示的运算程序中,若开始输入的x值为36,我们发现第1次输出的结果为18,第2次输出的结果为9,第2016次输出的结果为6.