题目内容
11.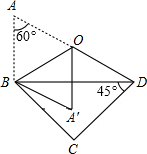 如图,一副三角板拼在一起,O为AD的中点,将△ABO沿OB折叠,点A落在A′的位置,点C在直线OA′上吗?为什么?
如图,一副三角板拼在一起,O为AD的中点,将△ABO沿OB折叠,点A落在A′的位置,点C在直线OA′上吗?为什么?
分析 连接OC.由直角三角形斜边上中线的性质可知OB=OA=OD,从而可证明△AOB为等边三角形,由翻折的性质可知∠BOA′=∠AOB=60°,然后证明△BOC≌△DOC,可求得∠BOC$\frac{1}{2}×120°$=60°,最后根据∠BDA′=∠BDC=60°可知点A′在OC上.
解答 解:点A′在OC上.
理由:如图所示:连接OC.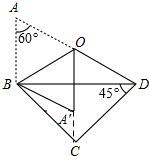
∵∠ABD=90°,O是AD的中点,
∴OB=OA=OD.
∵∠A=60°,OA=OB,
∴△AOB为等边三角形.
∴∠AOB=60°.
由翻折的性质可知:∠BOA′=∠AOB=60°.
∵∠AOB=60°,
∴∠BOD=120°.
在△BOC和△DOC中,$\left\{\begin{array}{l}{OB=OD}\\{BC=DC}\\{OC=OC}\end{array}\right.$,
∴△BOC≌△DOC.
∴∠BOC=∠DOC=$\frac{1}{2}∠BOD$=$\frac{1}{2}×120°$=60°.
∴∠BDA′=∠BDC.
∴点A′在OC上.
点评 本题主要考查的是翻折的性质、等边三角形的性质和判定、全等三角形的性质和判定、直角三角形斜边上中线的性质,证得∠BDA′=∠BDC是解题的关键.

练习册系列答案
相关题目
6.已知一次函数y=(m+1)x+m2-1(m为常数),若它的图象过原点,则( )
| A. | m=1 | B. | m=±1 | C. | m=-1 | D. | m=0 |
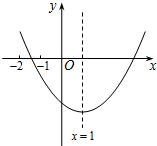 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②abc>0;③b=-2a;④9a+3b+c<0. 其中,正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②abc>0;③b=-2a;④9a+3b+c<0. 其中,正确结论的个数是( ) (1)如图,要搭建一个矩形的自行车棚,一边靠墙,另外三边围栏材料的总长为60m,怎样围才能使车棚的面积最大?
(1)如图,要搭建一个矩形的自行车棚,一边靠墙,另外三边围栏材料的总长为60m,怎样围才能使车棚的面积最大? 如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x+2分别交x轴、y轴于A、B两点,点P(1,m)在△AOB的形内(不包含边界),则m的值可能是1.(填一个即可)
如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x+2分别交x轴、y轴于A、B两点,点P(1,m)在△AOB的形内(不包含边界),则m的值可能是1.(填一个即可)