题目内容
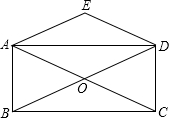 矩形ABCD的对角线AC,BD相交于点O,AE∥BD,DE∥AC.
矩形ABCD的对角线AC,BD相交于点O,AE∥BD,DE∥AC.(1)四边形AODE是什么特殊四边形?证明你的结论.
(2)若AC=4,∠ODE=60°,求四边形AODE的面积.
考点:矩形的性质,菱形的判定与性质
专题:
分析:(1)求出四边形AODE是平行四边形,再根据矩形的性质对角线互相平分且相等可得OA=OD,然后根据邻边相等的平行四边形是菱形解答;
(2)根据矩形的对角线互相平分求出OA,OB=OD,根据矩形的对角线相等可得BD=AC,再根两直线平行,同位角相等可得∠AOB=∠ODE,然后判断出△AOD是等边三角形,根据等边三角形的性质求出AB,再利用勾股定理列式求出AD,然后求出△ABD的面积,再根据等底等高的三角形的面积相等求出S△AOD,最后根据S四边形AODE=2S△AOD解答.
(2)根据矩形的对角线互相平分求出OA,OB=OD,根据矩形的对角线相等可得BD=AC,再根两直线平行,同位角相等可得∠AOB=∠ODE,然后判断出△AOD是等边三角形,根据等边三角形的性质求出AB,再利用勾股定理列式求出AD,然后求出△ABD的面积,再根据等底等高的三角形的面积相等求出S△AOD,最后根据S四边形AODE=2S△AOD解答.
解答:(1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵四边形ABCD是矩形,
∴OA=OD,
∴四边形AODE是菱形;
(2)解:∵四边形ABCD是矩形,
∴OB=OD=OA=
AC=
×4=2,BD=AC=4,
∵AC∥DE,∠ODE=60°,
∴∠AOB=∠ODE=60°,
∴△AOD是等边三角形,
∴AB=OA=2,
由勾股定理得,AD=
=
=2
,
∴S△ABD=
×2×2
=2
,
∵OB=OD,
∴S△AOD=
S△ABD=
×2
=
,
∴S四边形AODE=2S△AOD=2
.
∴四边形AODE是平行四边形,
∵四边形ABCD是矩形,
∴OA=OD,
∴四边形AODE是菱形;
(2)解:∵四边形ABCD是矩形,
∴OB=OD=OA=
| 1 |
| 2 |
| 1 |
| 2 |
∵AC∥DE,∠ODE=60°,
∴∠AOB=∠ODE=60°,
∴△AOD是等边三角形,
∴AB=OA=2,
由勾股定理得,AD=
| BD2-AB2 |
| 42-22 |
| 3 |
∴S△ABD=
| 1 |
| 2 |
| 3 |
| 3 |
∵OB=OD,
∴S△AOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴S四边形AODE=2S△AOD=2
| 3 |
点评:本题考查了矩形的性质,菱形的判定与性质,等边三角形的判定与性质,熟记矩形的对角线互相平分且相等以及菱形的判定方法是解题的关键.

练习册系列答案
相关题目
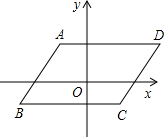 如图,平行四边形ABCD中,AD∥x轴,下列说法正确的是( )
如图,平行四边形ABCD中,AD∥x轴,下列说法正确的是( )| A、A与D的横坐标相同 |
| B、C与D的横坐标相同 |
| C、B与C的纵坐标相同 |
| D、B与D的纵坐标相同 |
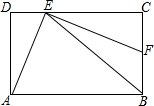 如图,在矩形ABCD中,BE平分∠ABC,交CD于点E,点F在BC边上
如图,在矩形ABCD中,BE平分∠ABC,交CD于点E,点F在BC边上