题目内容
 在半径为1的⊙O中,弦AB=
在半径为1的⊙O中,弦AB=| 2 |
| 3 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:垂径定理,含30度角的直角三角形,解直角三角形
专题:计算题
分析:过O作OD⊥AB,OE⊥AC,连接OA,过B作BF⊥OC,利用垂径定理得到D为AB中点,E为AC中点,即AD=BD,AE=CE,在直角三角形AOD与直角三角形AOE中,利用锐角三角函数定义及特殊角的三角函数值求出∠DAO与∠CAO的度数,进而求出圆周角∠BAC的度数,利用同弧所对的圆心角等于所对圆周角的2倍求出∠BOC的度数为30度,利用30度所对直角边等于斜边的一半求出BF的长,即可求出三角形BOC的面积.
解答: 解:过O作OD⊥AB,OE⊥AC,连接OA,过B作BF⊥OC,
解:过O作OD⊥AB,OE⊥AC,连接OA,过B作BF⊥OC,
∴D为AB中点,E为AC中点,即AD=BD=
,AE=CE=
,
在Rt△AOD中,OA=1,AD=
,
∴cos∠OAD=
,即∠OAD=45°,
在Rt△AOE中,OA=1,AE=
,
∴cos∠OAE=
,即∠OAE=30°,
∴∠BAC=∠OAD-∠OAE=15°,
∴∠BOC=30°,
在Rt△BOF中,BF=
OB=
,
则S△BOC=
OC•BF=
.
故选A
 解:过O作OD⊥AB,OE⊥AC,连接OA,过B作BF⊥OC,
解:过O作OD⊥AB,OE⊥AC,连接OA,过B作BF⊥OC,∴D为AB中点,E为AC中点,即AD=BD=
| ||
| 2 |
| ||
| 2 |
在Rt△AOD中,OA=1,AD=
| ||
| 2 |
∴cos∠OAD=
| ||
| 2 |
在Rt△AOE中,OA=1,AE=
| ||
| 2 |
∴cos∠OAE=
| ||
| 2 |
∴∠BAC=∠OAD-∠OAE=15°,
∴∠BOC=30°,
在Rt△BOF中,BF=
| 1 |
| 2 |
| 1 |
| 2 |
则S△BOC=
| 1 |
| 2 |
| 1 |
| 4 |
故选A
点评:此题考查了垂径定理,圆周角定理,以及含30度直角三角形的性质,熟练掌握垂径定理是解本题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
已知两圆的半径分别为6和4,圆心距为2,则两圆的位置关系是( )
| A、相交 | B、内含 | C、外切 | D、内切 |
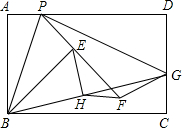 在远古时代,我们的祖先就发现并证明了在直角三角形中斜边上中线等于斜边的一半,今天的我们可以直接运用.现有一张长方形纸片ABCD,在AD边上任取一点P(不与点A、点D重合),以BP所在直线为折痕,将长方形如图翻折,使A点翻到E点,再将PD翻到与PE所在直线位置重合,得到折痕PG,PG与DC边交于点G,点D翻到点F处,如图,连接BG,取BG的中点H,连接HE、HF,试猜想线段HE与HF之间的大小关系,并说明理由.
在远古时代,我们的祖先就发现并证明了在直角三角形中斜边上中线等于斜边的一半,今天的我们可以直接运用.现有一张长方形纸片ABCD,在AD边上任取一点P(不与点A、点D重合),以BP所在直线为折痕,将长方形如图翻折,使A点翻到E点,再将PD翻到与PE所在直线位置重合,得到折痕PG,PG与DC边交于点G,点D翻到点F处,如图,连接BG,取BG的中点H,连接HE、HF,试猜想线段HE与HF之间的大小关系,并说明理由. 已知反比例函数y1=
已知反比例函数y1= 现有一张演唱会的票,小明和小亮两人都想去.于是两想了个办法.用如图所示的两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成3等分,每份分别标有1,3,6这三个数字;转盘B被均匀地分成4等分,每份分别标有2,4,5,7这四个数字.①同时自由转动转盘A和B;②转盘停止后,指针各指向一个数字(如果指针恰好指在分格线上,那么重转一次,直到指针指向某一数字为止),用所指的两个数字相乘,如果积为偶数,小明去,否则小亮去.这个方法公平吗?请你说明理由.若不公平,请你帮忙修改一个公平的规则.
现有一张演唱会的票,小明和小亮两人都想去.于是两想了个办法.用如图所示的两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成3等分,每份分别标有1,3,6这三个数字;转盘B被均匀地分成4等分,每份分别标有2,4,5,7这四个数字.①同时自由转动转盘A和B;②转盘停止后,指针各指向一个数字(如果指针恰好指在分格线上,那么重转一次,直到指针指向某一数字为止),用所指的两个数字相乘,如果积为偶数,小明去,否则小亮去.这个方法公平吗?请你说明理由.若不公平,请你帮忙修改一个公平的规则.