Question

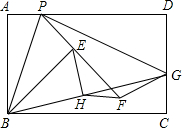在远古时代，我们的祖先就发现并证明了在直角三角形中斜边上中线等于斜边的一半，今天的我们可以直接运用．现有一张长方形纸片ABCD，在AD边上任取一点P（不与点A、点D重合），以BP所在直线为折痕，将长方形如图翻折，使A点翻到E点，再将PD翻到与PE所在直线位置重合，得到折痕PG，PG与DC边交于点G，点D翻到点F处，如图，连接BG，取BG的中点H，连接HE、HF，试猜想线段HE与HF之间的大小关系，并说明理由．

Answer 1

考点：翻折变换（折叠问题）,直角三角形斜边上的中线

专题：

分析：如图，延长FH交BE于点M．构建全等三角形△BMH≌△GFH，然后运用“直角三角形斜边上的中线等于斜边的一半”进行证明结论．

解答：解：HE=HF．理由如下：
如图，延长FH交BE于点M．
根据折叠的性质知，∠PEB=∠A=90°，∠PFG=∠D=90°，
又∵∠PEB+∠BEF=180°
∴∠BEF=90°，
∴∠BEF=∠PFG=90°，
∴BE∥FG，
∴∠MBH=∠HGF，
∵H为BG的中点，
∴BH=GH，
∴在△BMH与△GFH中，

∠MBH=∠HGF BH=GH ∠MHB=∠FHG(对顶角相等)

，
∴△BMH≌△GFH（ASA），
∴MH=FH=

1

2

FM．
∵∠MEF=90°，
∴EH=

1

2

FM，
∴HE=HF．

点评：本题综合考查了图形变换的性质，逻辑推理能力以及探究能力．会熟练运用全等三角形的判定与性质和直角形斜边上的中线解题是基本的数学能力．