题目内容
 已知反比例函数y1=
已知反比例函数y1=| k |
| x |
(1)求k的值,并在平面直角坐标系中画出y1=
| k |
| x |
(2)方程x2+bx-k=0的根可看做y1=
| k |
| x |
考点:反比例函数与一次函数的交点问题,反比例函数的图象,待定系数法求反比例函数解析式
专题:计算题
分析:(1)把A点坐标代入反比例函数解析式中可求出k的值,然后画图象;
(2)先由横坐标为2和4,根据反比例函数解析式得到交点坐标为点(2,4)和点(4,2),然后把交点坐标分别代入y=x+b可得到b的范围.
(2)先由横坐标为2和4,根据反比例函数解析式得到交点坐标为点(2,4)和点(4,2),然后把交点坐标分别代入y=x+b可得到b的范围.
解答:解:(1)把A(2,4)代入y=
得k=2×4=8,如图,
(2)∵方程x2+bx-k=0的一个实根为m,且满足2≤m≤4,
∴y1=
的图象与y2=x+b的图象交点的横坐标在2到4之间,在反比例函数图象为点(2,4)和点(4,2)之间,
把点(2,4)和点(4,2)代入y=x+b得b=2或b=-2,
∴b的范围为-2≤b≤2.
故答案为-2≤b≤2.
| k |
| x |

(2)∵方程x2+bx-k=0的一个实根为m,且满足2≤m≤4,
∴y1=
| k |
| x |
把点(2,4)和点(4,2)代入y=x+b得b=2或b=-2,
∴b的范围为-2≤b≤2.
故答案为-2≤b≤2.
点评:本题考查了反比例函数一次函数的交点问题:反比例函数与一次函数的交点坐标满足两函数的解析式.

练习册系列答案
相关题目
如果(a-1)-2=1成立,则( )
| A、a≠1 | B、a=0 |
| C、a=2 | D、a=0或a=2 |
 在半径为1的⊙O中,弦AB=
在半径为1的⊙O中,弦AB=| 2 |
| 3 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 一个圆锥的母线长为12cm,底面半径为4cm.如图,O为圆锥的顶点,M为圆锥底面上一点,点P是OM的中点.一只蜗牛从P点出发绕圆锥侧面爬行,回到P点时所爬过的最短路线的长度是( )
一个圆锥的母线长为12cm,底面半径为4cm.如图,O为圆锥的顶点,M为圆锥底面上一点,点P是OM的中点.一只蜗牛从P点出发绕圆锥侧面爬行,回到P点时所爬过的最短路线的长度是( )| A、8πcm | ||
| B、4πcm | ||
C、6
| ||
| D、6cm |
 如图,在数轴上A、B两点的距离等于( )
如图,在数轴上A、B两点的距离等于( )| A、2 | B、3 | C、4 | D、-2. |
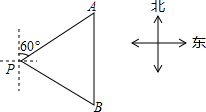 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行80海里后,到达B处,求此时轮船所在的B处相对于灯塔P的位置.(结果保留根号)
如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行80海里后,到达B处,求此时轮船所在的B处相对于灯塔P的位置.(结果保留根号)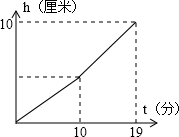 一个容器由上下竖直放置的两个圆柱体A,B连接而成.向该容器内匀速注水,容器内水面的高度h(厘米)与注水时间t(分)的函数关系如图所示.若上面A圆柱体的底面积是300厘米2,下面圆柱体B的底面积是500厘米2.则每分钟向容器内注水
一个容器由上下竖直放置的两个圆柱体A,B连接而成.向该容器内匀速注水,容器内水面的高度h(厘米)与注水时间t(分)的函数关系如图所示.若上面A圆柱体的底面积是300厘米2,下面圆柱体B的底面积是500厘米2.则每分钟向容器内注水